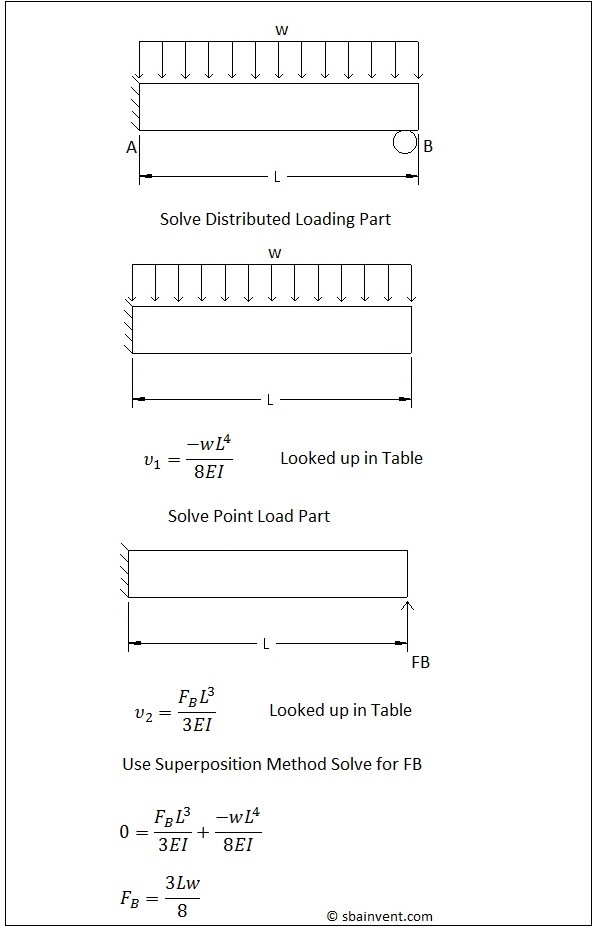
Statically indeterminate means that the beam has more unknown forces then there are statics equations to solve for those unknowns. Typically, a beam can have a possible 3 equations to describe it statically if it is treated as a 2 dimensional problem. These equations would be one for the x direction, one for the y direction, and one moment equation.
There are few ways that a statically indeterminate beam can be solved. It can be solved by using methods of integration. The superposition method can also be used to solve the problem.
Methods of Integration
The same process that was used to determine the beams deflection would be used to solve a statically indeterminate beam. First, the moment diagram and its corresponding equations have to be derived. After that has been found, the moment equation would be integrated twice. From that you would have to use a set of boundary conditions to solve for the C constants, as well as the unknown forces. Refer to the example below.

The Superposition Method
The superposition method is another method that can be used to solve a statically indeterminate beam problem. Basically, the superposition method will split a statically indeterminate problem into separate statically determinate problems. Those solutions are then added together, as seen in the figure below.
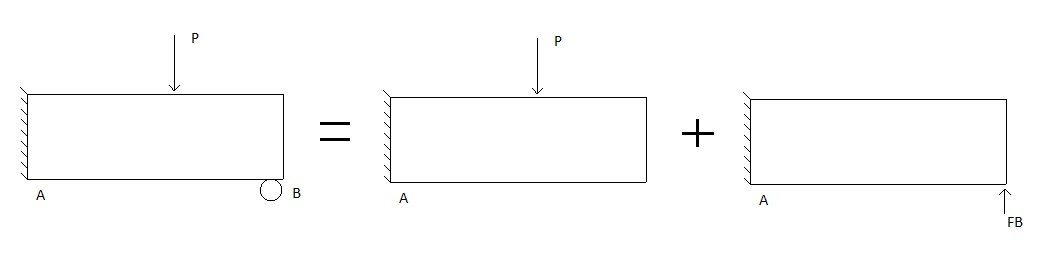
Adding the two solutions together will then make it possible to create an additional equation to solve for the unknown force. The main advantage of using superposition method is that you can use tables found in most books to look up basic deflection equations. By using those table the steps a greatly reduced. Of course if there aren’t any tables available than different beam deflection methods could be used to derive the deflection equations that would be needed.
To solve for an unknown force using superposition method refer to the example below.