Some people I’ve notice like to use the words Stress and Strain interchangeably, which they are not.
Stress represents how much force an object can withstand over a certain area. Since stress is a force over an area, the units are the same units that represent pressure. Which really means stress is the amount of pressure on an object. This is than used to determine when the object would start to deform and than ultimately fail. These are know as the yield strength of the material and the ultimate stress of the material. This will be talked about in a different section.
Strain on the other hand is unitless number that represents the change in length of a piece of material over its original length. Knowing how to calculate strain is also important since even though the object may not have failed sometimes knowing how much it has deformed is important to. The reason why is because the deforming object could cause issues with other components depending upon how much it has deformed.
Both stress and strain can be related to one another through Hook’s Law.
(Eq 1) $σ=Eε$
σ = stress
ε = strain
E = Young’s Modulus
Stress
Stress is a very important variable in solid mechanics. It is used to determine the amount of pressure that can be put on a part before it will start to yield as well as when it will ultimately break .
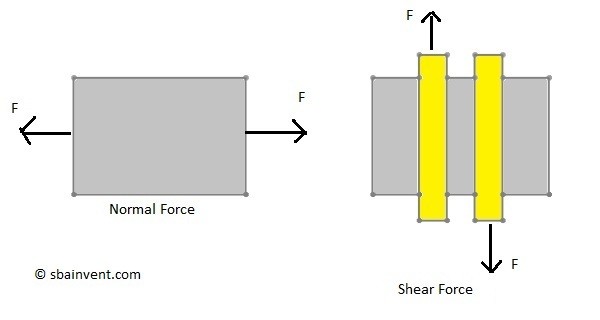
There are two general types of stresses that can be put on a part. These are shear stress and normal stress. When an object is under shear there is force on the part that is is applied perpendicular to a given axis. Normal stress on the other hand is cause by a force that is either pulling or pushing in parallel to a given axis. Refer to the image below.
(Eq 2) $σ=\frac{F}{A}$
σ = normal stress
F = force
A = area
(Eq 3) $τ=\frac{F}{A}$
τ = shear stress
Now besides the two general forms of stress, there are more specific names for stress. They are the following. For normal stress, there is axial stress , and normal bending stresses. For shear stress there is torsional stress, and transverse shear stress. Finally, in addition to these there are also stress concentrations . These will be discussed in other sections.
Strain
Strain is a unitless number that is used to determine how much an object will deflect due to a given stress. There are few reasons why it might be important to determine the strain on a part due to a given load. First, if an object deflects to much due to a load, it could interfere with other parts. Also, another reason why strain in important is because it can be used to calculate a stress during an experiment. Hooke’s law would be used to calculate the stress due to a given strain as seen in the equation below.
(Eq 4) $σ=Eε$
σ = stress
ε = strain
E = Young’s Modulus
To calculate strain, the change in length of the part needs to be determined due to the applied load. This is than divided by the original length of the part. See the equations below.
(Eq 5) $ε=\frac{L’-L}{L}=\frac{ΔL}{L}$
ε = normal strain
L = original length
L’ = new length
ΔL = change in length
(Eq 6) $γ=\frac{π}{2}-Δθ$
γ = shear strain
Δθ = change in angle (radians)
Now in real life why are the above equations important? The answer to this is simple. During an experiment it is easier to determine the change of length of part due to loading by using a strain gauge. These values would than be used to determine the stress on the part, which can than be used to validate your analytical analysis.