It is known that an object will contract or expand when the temperature changes. This contraction and expansion process can cause a thermal stress on an object if there is an interference from contacting another part, or if the part is made out of different types of materials.
All translational directions (x, y, and z) are effected by thermal expansion during the expansion or contraction process. I will only be talking about thermal expansion in one direction.
Before you can start solving for stresses you need to know how to calculate thermal expansion. To calculate thermal expansion the equations below would be used.
(Eq 1) $δ_T=αΔTL$
$α=linear~coefficient~of~thermal~expansion~units~\frac{1}{^oC}~or~\frac{1}{^oF}$
(Eq 2) $δ_T=∫_0^LαΔTdx$
Below you can see the coefficient of thermal expansion for a few different types of material.
| Material | |
|---|---|
Now that you know how to calculate thermal expansion you now need to know how that can cause a stress on a part. Generally it the part isn’t made out of materials with different rates of thermal expansion or there isn’t an interference due to thermal expansion there won’t be a resulting stress. However, if there is, there will be a resulting stress, and the problem will be statically indeterminate. Below is an example on how to calculate a simple thermal stress on a part due to thermal stress for an increase in temperature.
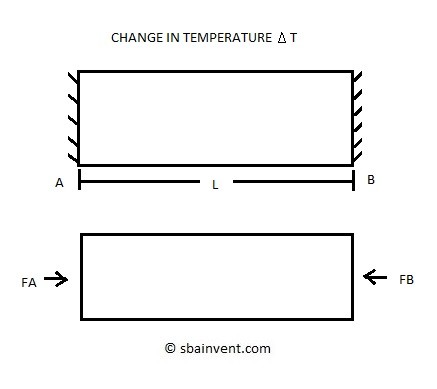
For the above problem the resulting statics equation can be seen below.
(Eq 3) $F_A-F_B=0$
$Where~F_A=F_B=F$
It can be seen that the above equation isn’t much help in determining the stress caused by thermal expansion. However, we do know that the part wants to expand which will put the part under compression. In order to do that we need to relate stress and strain using Hook’s Law, while integrating the thermal expansion equation into Hook’s law. Refer to the equation below to see how this is accomplished.
(Eq 4) $αΔTL-\frac{FL}{EA}=0$
Solving for the force F in equation 4 will result in the following equation.
(Eq 5) $F=αΔTEA$
Finally, to find the stress caused by thermal expansion equation 6 would be used.
(Eq 6) $σ=αΔTE$