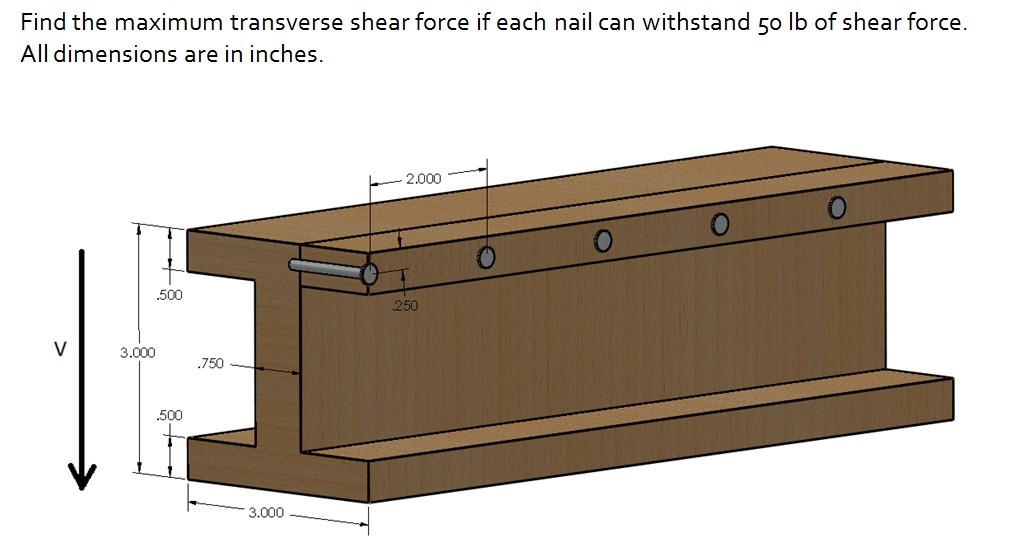
Before continuing on if you don’t have an understand of shear and moment diagrams and how to calculate the area moment of inertia. I strongly recommend that you look at those pages before continuing.
Bending consists of a normal stress and a shear stress. Typically an engineer is more interested in the normal stress, since normally that stress is more prominent. However, there are cases where a beam could be short and stubby which in that case the shear stress becomes more influential.
Transverse Shear
The shear stress due to bending is often referred to as transverse shear. Like the normal stress there is a stress profile that is based off of the neutral axis of the particular cross-sectional area. Unlike normal stress, the highest stress value occurs at the neutral axis, while there is no stress on the walls. Refer to the figure below to view a typical stress profile.
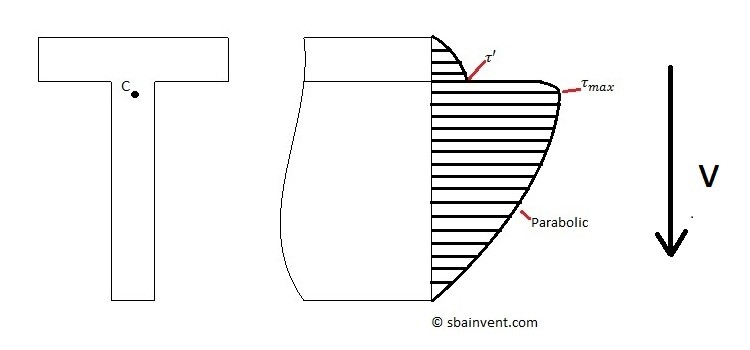
In order to calculate the shear stress at different location on the stress profile equation 1 would be used.
(Eq 1) $τ=\frac{VQ}{Iw}$
$V$ = Shear Force
$I$ = Area Moment of Inertia
$w$ = the width of the cross-section
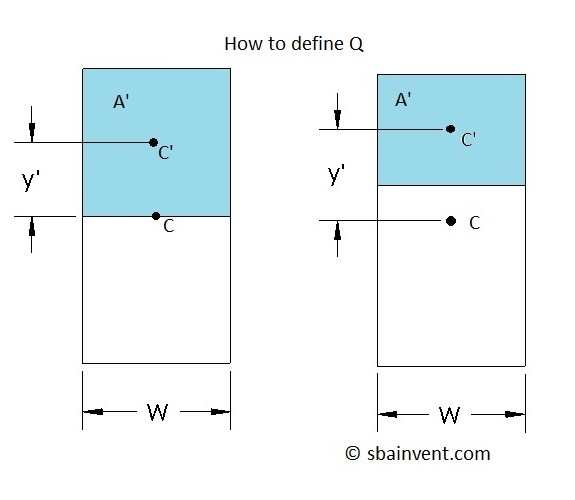
Notice in equation 1 that there is term defined by Q. Q is basically a representation of the area above the point of interest in relation to that area’s centroid and the main cross-section centroid. Q is defined by equation 2.
(Eq 2) $Q=\int_{A’}ydA’=y’A’=\sum{}y’A’$
Also, refer to the figure below to get a better idea of what Q is in relation to equation 2.
Shear Flow
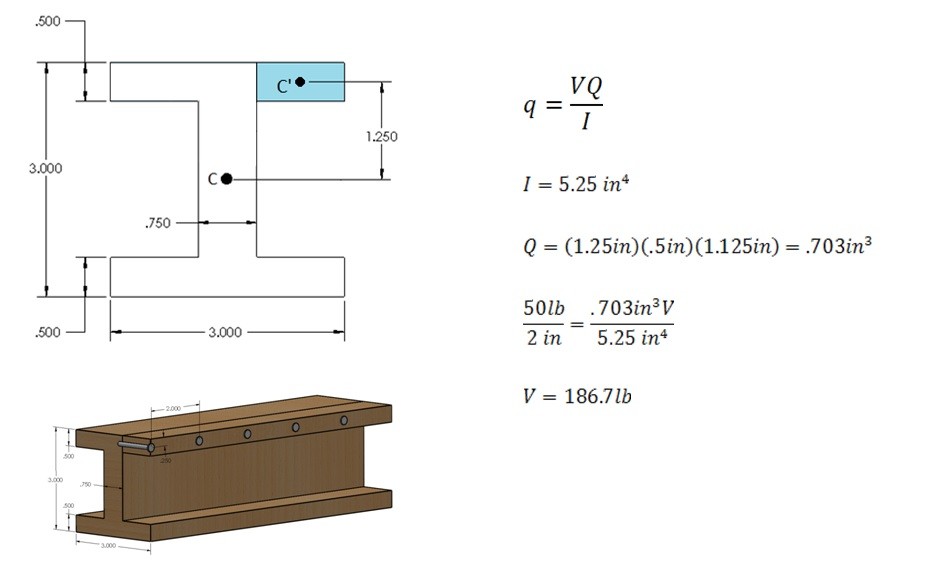
Shear flow is the measurement of shear force per length. The reason why an engineer might want to calculate the shear flow is because if there are bolts holding pieces of the beam together, shear flow can be used to calculate the shear force on each bolt. To calculate shear flow on a beam from transverse shear equation 3 would used. Refer to the example below.
(Eq 3) $q=\frac{VQ}{I}$