There are few ways that the deflection of a beam can be determined due to the loading that is placed on it. I am going to discuss how to use integration and discontinuity functions. In corresponding articles. However, before you go any further, if you do not know how to generate a moment diagram, or how to calculate the area moment of inertia I suggest you go to those reference pages first.
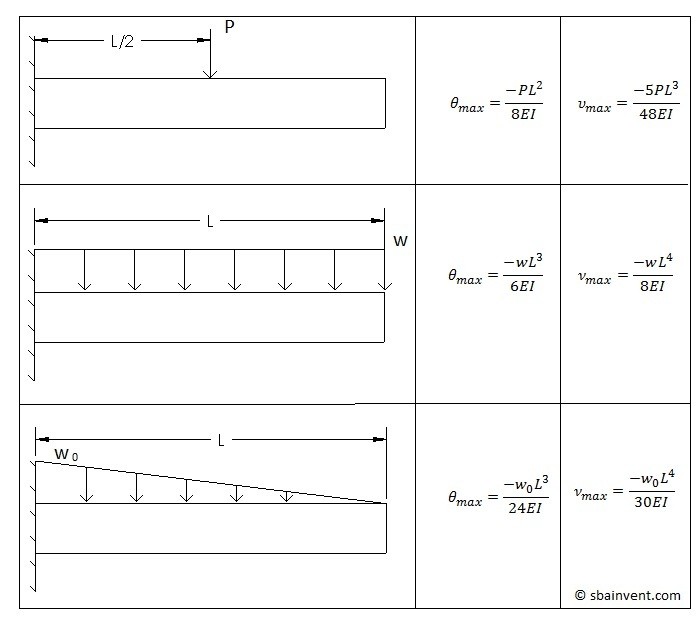
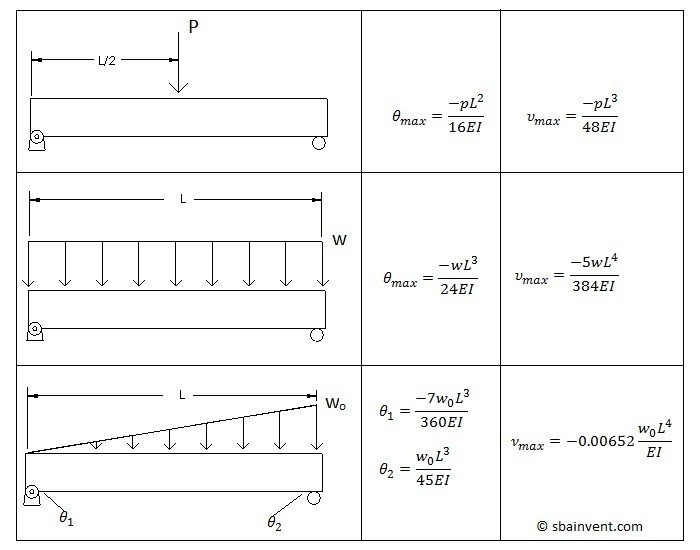
The tables below provide the maximum deflection and slope for 6 unique setups.
.Deflection by Integration
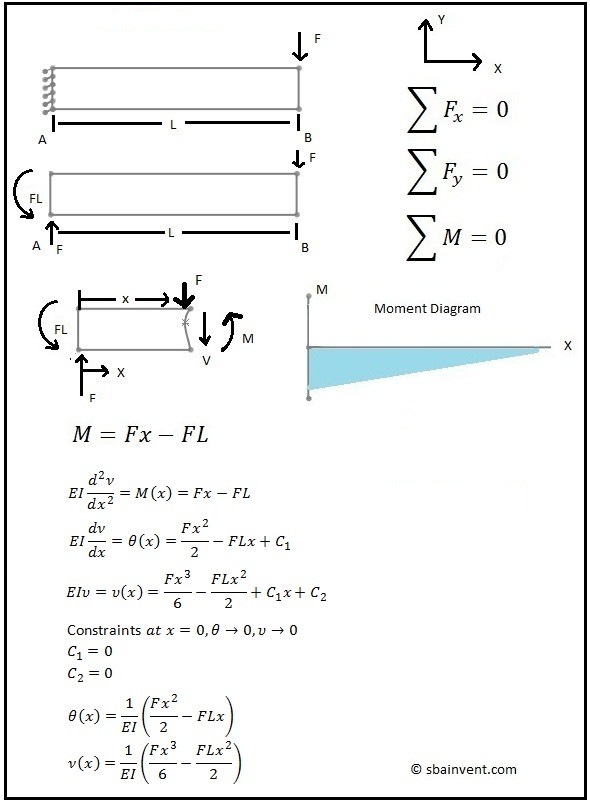
If you know what the moment equation is that represents the particular beam of interest then you can take a double integral to determine what the deflection of the beam is. The first integration will represent the slope of the beam, while the second will represent the deflection.
Before I go any further on this subject though, you need to understand some basic calculus. For the most part all you will have to deal with is polynomial functions. Refer to equation 1 to see how to perform a basic polynomial integral.
(Eq 1) $\int x^pdx=\frac{x^{p+1}}{p+1}+C$
$p$ = some power ranging from $0\rightarrow∞$
$C$ = some constant
To reverse an integral you would take the derivative of the function; equation 2.
(Eq 2) $\frac{d}{dx}x^p=px^{p-1}$
$\frac{d}{dx}$ symbolizes derivative for variable x
$\frac{d^2}{dx^2}$ symbolizes double derivative for variable x
Another thing that has be considered when relating the moment equation to deflection is the Young’s modulus of the material. The reason for this is because of Hook’s law relates stress and strain, so effectively the Young’s modulus is used to transform stress to strain so that a deflection can be determined. Equations 3-5 shows how to use calculus and Young’s modulus, along with beam theory to determine the deflection and slope from the moment.
(Eq 3) $EI\frac{d^2v}{dx^2}=M(x)$
(Eq 4) $EI\frac{dv}{dx}=θ(x)$
(Eq 5) $EIv = v(x)$
$v$ = deflection
$θ$ =slope
An example is shown below.
Discontinuity Functions
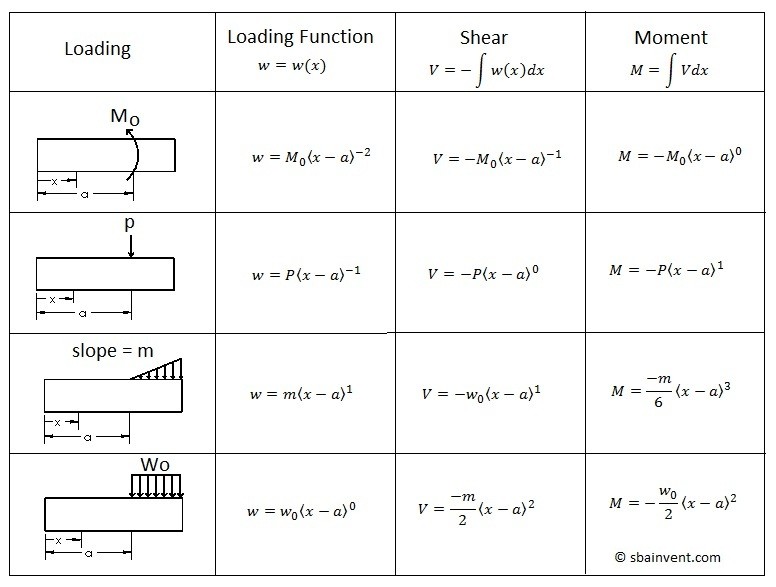
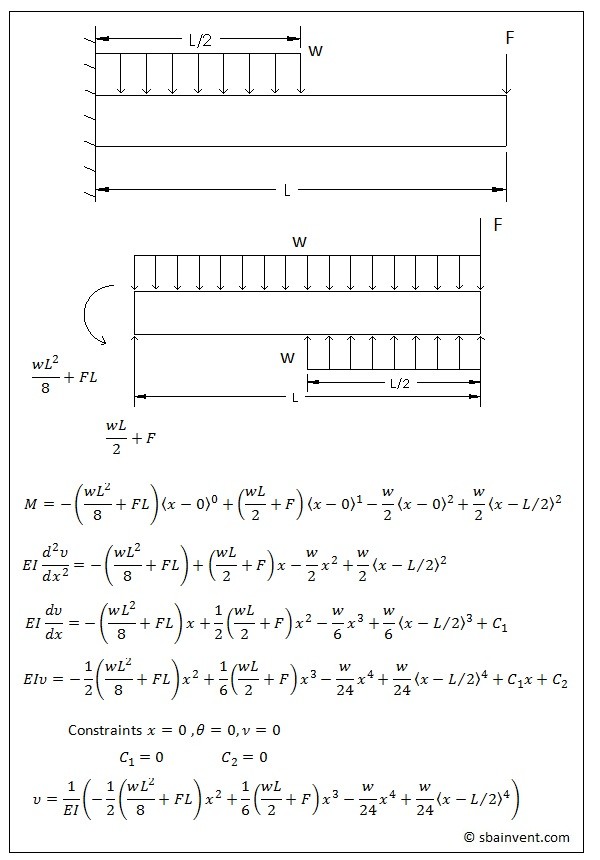
Another method that can be used to determine the deflection is to use the discontinuity functions; also known as the Macaulay Functions. The discontinuity functions are used to bypass the step of making a moment diagram to determine the moment. It does this by using the equations found in the table below and taking in consideration that the forces placed on the beam can be related to the deflection of the beam through calculus, as well as the shear forces.Refer to equation 6-7.
(Eq 6) $EI\frac{d^4v}{dx^4}=-w(x)$
(Eq 7) $EI\frac{d^3v}{dx^3}=V(x)$