Torsion is caused by a twisting moment called torque. In order to calculate torque you would have to multiply the applied forced that is perpendicular to the centroid by the distance from the centroid. For a cylinder the distance from the centroid would the radius of the cylinder. To calculate torque, equation 1 would be used and refer to the image below.
(Eq 1) $T=FD$
T = Torque
F = Perpendicular Force
d = Distance from Central Axis
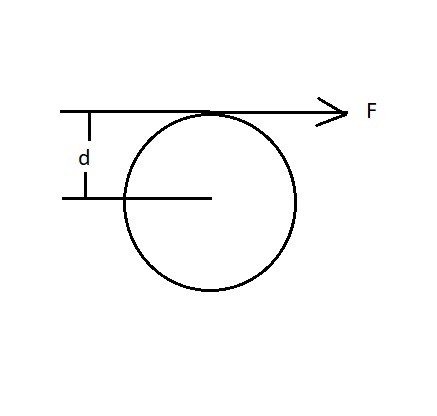
From the above it can be seen that torque will increase as you increase the distance from the centroid, while alternatively the torque will decrease for the same force if the distance from the centroid decreases. The fact that this happens is what makes gearing systems work.
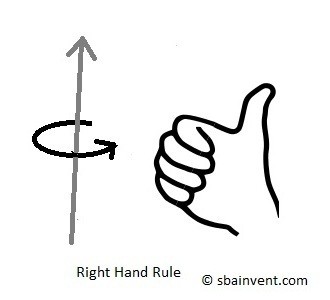
Torque can be negative or positive depending on the direction of the torque. Torque that is positive goes in the counter-clockwise direction; negative torque goes in the clockwise direction. If you’re confused use your right hand and point your thumb towards yourself, the way your fingers curl represents a positive torque. This is called the right hand rule. The figure a shown above shows a negative torque, while the figure below shows a positive torque.
Torsional Stress
All stress caused by torsion is shear stress. For a circular rod, maximum stress is found on the surface, and it decreases linearly to zero as you approach the central axis, refer to the figure below. For objects that are not circular the resulting stress field is different. This will be discussed in another section.
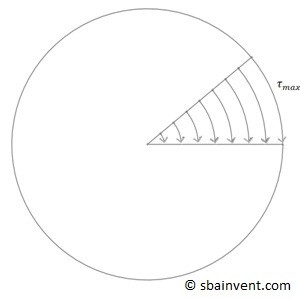
In order to calculate the maximum shear stress on a rod due to torque the equation below would be used.
(Eq 2) $τ_{max}=\frac{Tr_o}{J}$
$τ_{max}$ = maximum shear stress
$r_o$ = outer radius
$J$ = polar moment of inertia
Notice from equation 2 that there is a variable J called Polar moment of inertia. The reason why the polar moment of inertia is included in the equation above is because it represents the ability of the specific shape to resist torsional deformation. This value has no dependence on the material properties of the given object. To calculate the polar moment of inertia for a circular rod equation 3 would be used.
(Eq 3) $J=\frac{π}{2}\left(r_o^4-r_i^4 \right)$
For the above equation ri goes to 0 if the cylinder is solid. If the cylinder is a tube ri is the inner radius of the tube.
Angle of Twist
For any applied stress to an object there must also be a resulting deflection of the object. In the case for torsion it would be a twisting motion called the angle of twist. In order to determine the angle of the twist Hook’s law would be used. The resulting equation can be seen below.
(Eq 4) $Φ=\frac{TL}{JG}$
L=length
G=shear modulus
When using equation 4 the length L is distance from the applied torque to the contrained point of the part. It isn’t the entire length of the part.