Statics is the study of how forces interact on a body. What statics does is it takes in consideration of Newton’s Law “For every action there is an equal and opposite reaction.” The law works because for every force applied to the object for it to be static (unable to move or rotate) there has to be an opposite and equal force to hold the object stationary.
Now you’re probably saying why do I need to know this information? The answer is simple, you need to know how to solve a statics problem to do more advanced problems, such as strength of material problems. Statics is basically the book keeping method that an engineer uses to solve problems.
I’m not going to go to crazy talking about statics on this website. Instead I’m going to create a basic overview of it that will apply to other sections of this website. Basically, I am going to discuss what type of forces and constraints could be placed on an object. I’m going to show you how to construct a correct free body diagram. I’m also going to show you how to deal with forces that are applied at an angle to the part. Finally, I’m going to discuss three dimensional forces.
Types of Loading
There are different types of forces that can be placed on an object. An object could have a point load placed on it, a distributed load, or a moment.
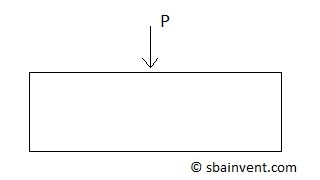
Point Load
A point load is a load that is placed on an infinitely small point on a object. Point loads are typically represented in the x, y, or z direction on a part. To view what a point load looks like refer to the figure below.
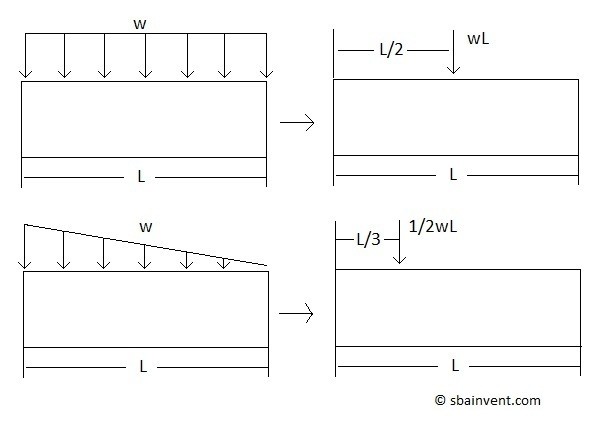
Distributed Load
A distributed load is a force/(unit length). When dealing with distributed load it is best to transform it into a point load. To do this you would have to calculate the area under the curve of the distributed load and you would also need to determine where the point load would occur on the object. Two common types of distributed loads are rectangular distributed loads and triangular distributed loads. Refer to the figures below.
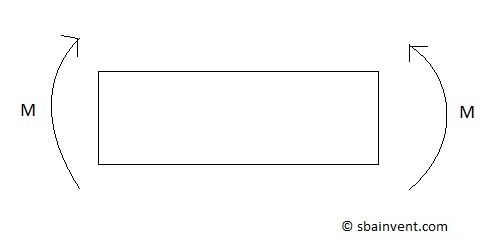
Moments
Moments represent rotational forces. A three dimensional problem can have up to three summed moments on it. You would calculate a moment the same way that a torque would be calculated, which would be the force times the perpendicular length. The difference between a moment and a torque is that a torque represents twisting while a moment represents bending. To view what a moment would look like refer to the figure below.
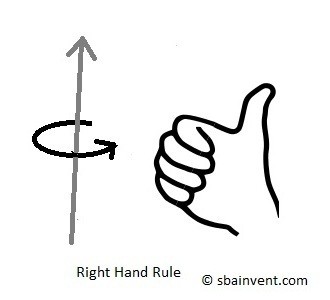
Types of Constraints
All Statics problems have constraints. There are three different types of constraints, fixed, pinned, and rolling. From these constrains it is possible that there could be a total of six resultant forces and moments for a 3d problem, which means the maximum number of statics equations that can be used to describe a problem would be six.
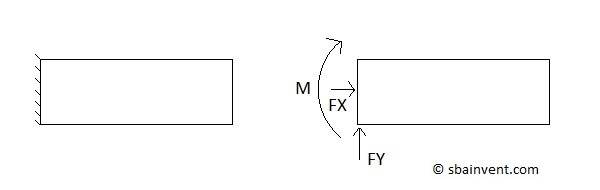
Fixed Constraint
A fixed constraint keeps an object from rotating and translating. Due to those constraints there will be reaction forces and moments in a all directions on that constraint. Refer to the figure below.
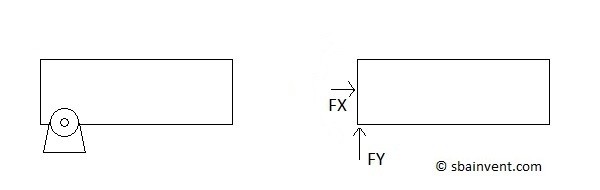
Pinned Constraint
Pinned constrains are constraints that prevent translation in all direction, but allow a rotation about the pin. This in turn will cause resultant forces but there will be no resultant moment for a two dimensional problem. Refer to the figure below.
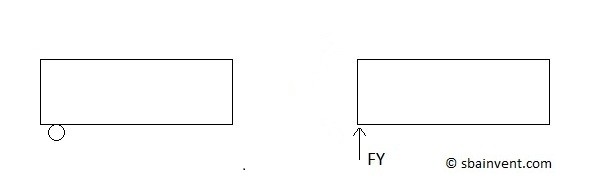
Rolling Constraint
A rolling constraint prevents translation in one direction. All other directions and rotations are not constrained, which means there will be only one resultant force due to that constraint. Refer to the figure below.
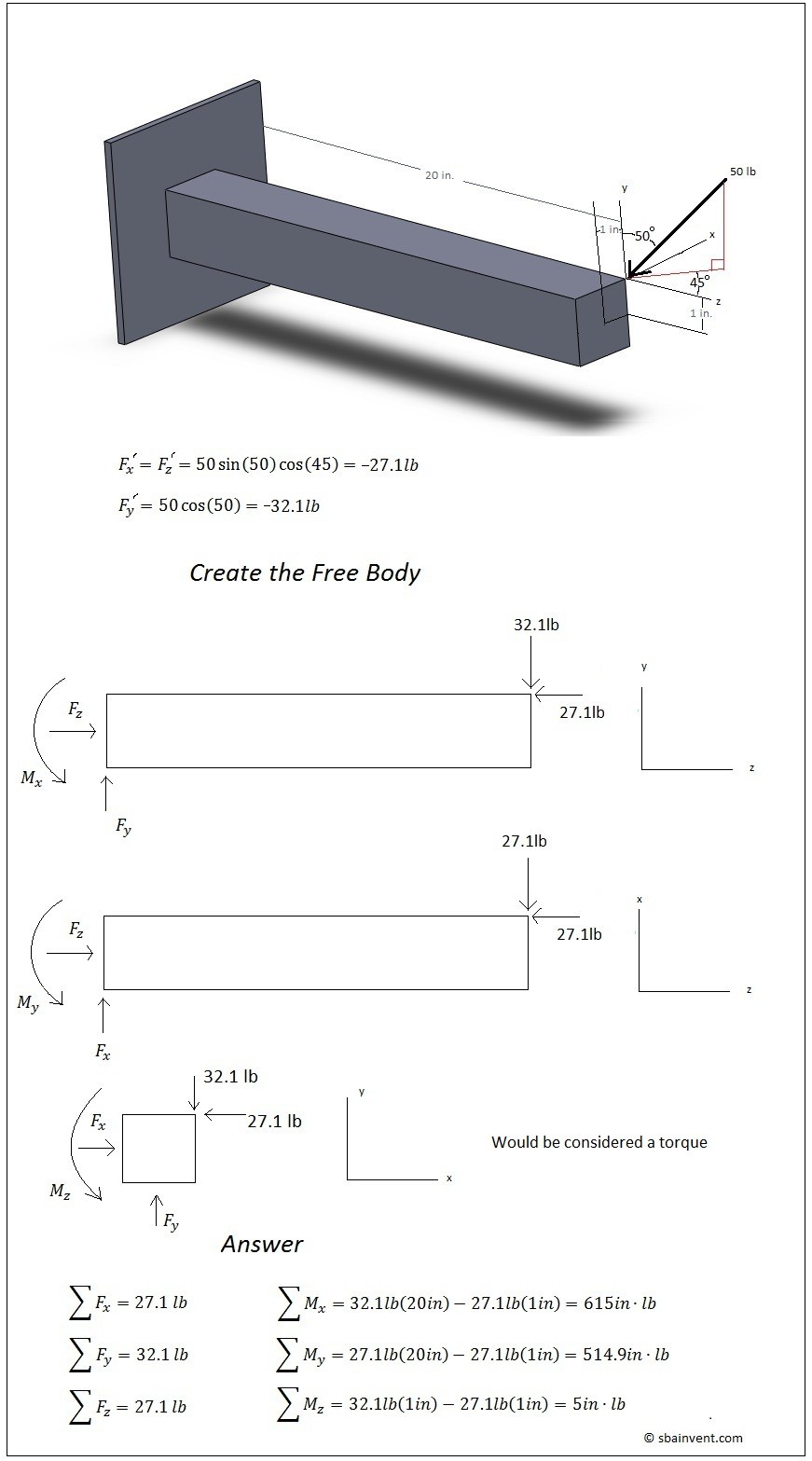
Free Body Diagrams
Free body diagrams are the book keeping for statics problems. If a free body diagram is drawn correctly it will allow the statics equations to be derived easier. Then it would be as simple as solving simultaneous equations to solve for the forces and moments at the constraints. Remember though only six possible equations are available to solve for the unknown constraint forces and moments for a 3d model. If there are more unknown forces then there are statics equations to solve for them then the problem would be considered statically indeterminate, which is discussed in the strength of materials section.
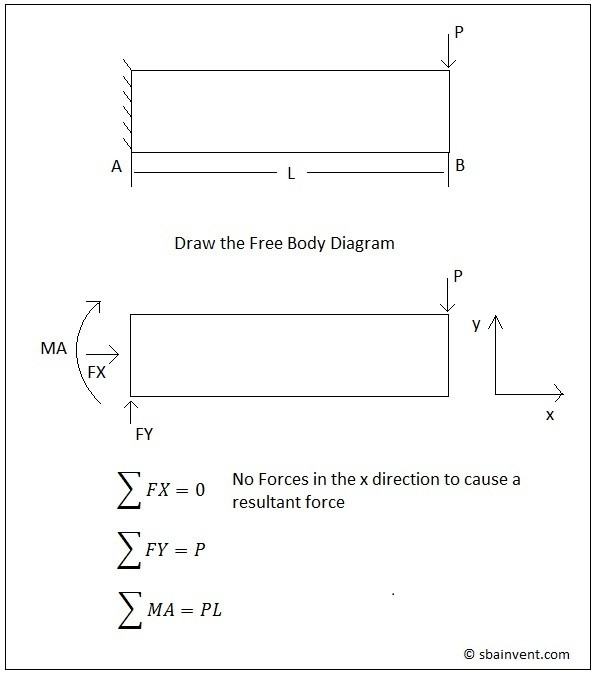
To setup a free body diagram for a problem and derive its statics equations (equations 1-6) refer to the example below.
(Eq 1) $∑x=0$
(Eq 2) $∑y=0$
(Eq 3) $∑z=0$
(Eq 4) $∑M_x=0$
(Eq 5) $∑M_y=0$
(Eq 6) $∑M_z=0$
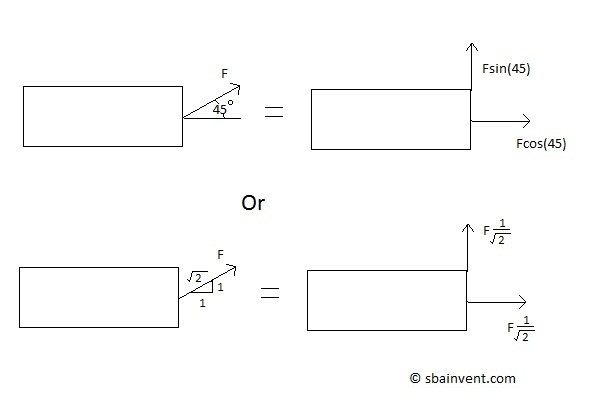
Offset Forces
When solving a statics problem, there can be times when the force applied may be at an angle to the coordinate system. Typically when solving a statics problem you would want to solve for forces that are purely in the x, y, and z directions. To solve a problem like this you would have to either reorient your coordinate system, or you would have solve for the amount of force that is in the particular directions that are affected.
When you have a force that is at an angle it can be represented in to different ways. First, that angle of orientation could be stated. But, in some cases there would be a right angle triangle with different number values along the legs and hypotenuse of the triangle. Those values state the contribution of the force in each direction. Refer to the figure below.
Magnitude and Angle
In addition to being able to calculate the forces in the x, y, and z directions, sometimes you may want to calculate the magnitude of all of those forces combined and the angle that the force is offset from the coordinate system. To calculate the magnitude equation 7 would be used. To calculate the orientation based off of the x-axis for a 2 dimensional problem equation 8 would be used.
(Eq 7) $F_M=\sqrt{F_x^2+F_y^2+F_z^2}$
(Eq 8) $tan^{-1}\left(\frac{y}{x}\right)$
3D Statics Problems
So far all that has been discussed is how to solve a two dimensional statics problem. However, in real life most problems are going to be 3d. To solve a 3d statics problem you would have to follow the same steps that you would used to solve a 2d statics problem, except in this case there is one more dimension that needs to be considered.
Also, when a problem is 3 dimensional it can have up to 6 possible statics equations to describe it. Those equations represent the summation of forces in the x, y, and z direction and the summation of moments around the x, y, and z axis. Refer to equations 1 through 6 below.
(Eq 9) $∑x=0$
(Eq 10) $∑y=0$
(Eq 11) $∑z=0$
(Eq 12) $∑M_x=0$
(Eq 13) $∑M_y=0$
(Eq 14) $∑M_z=0$