A thin wall pressure vessel is a container that is under pressure that is considered to have a thin wall. To classify as a thin wall pressure vessel, the inner radius r is more than or 10 times greater than the thickness t; r/t > 10. If r/t = 10 then the predicted stress can be up to 4 % less than the actual stress. This error is due to the fact that as the thickness grows in relationship to the inner radius, there will be a greater variation of stress across the thickness. However, if it is said to be a thin wall pressure vessel then the stress difference isn’t significant and it can be assumed as uniform.
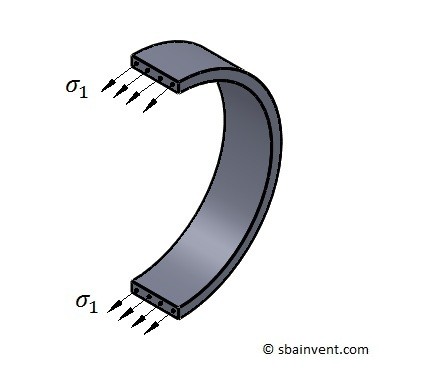
When a thin wall pressure vessel is under stress, there can be multiple stresses that need to be considered. The first stress is called the circumferential or hoop stress. Refer to the figure and equation 1 below.
(Eq 1) $σ_1=\frac{pr}{t}$
$p$ = gauge pressure
$r$ = radius
$t$ = thickness
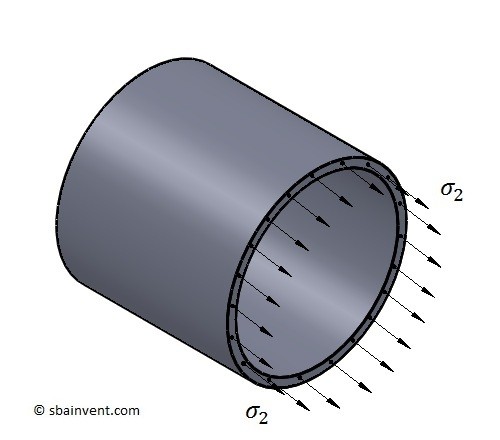
(Eq 2) $σ_2 = \frac{pr}{2t}$
Types of Pressure Vessels
There are different types of pressure vessels, but the two that will be discussed here are cylinders and spheres. A pressure vessel that is cylindrical in shape has both a hoop stress and a longitudinal stress. The hoop stress however is normally always two time greater than the longitudinal stress. Due to this, hoses and other cylindrical type vessels will split on the wall instead of being pulled apart like it would under an axial load. Refer to the picture below.