When you are using Bernoulli equation you will need to realize that you will be analyzing different types of pressure. These types of pressure are static pressure, dynamic pressure, stagnation pressure, and total pressure.
Static Pressure
Static pressure is a pressure that occurs independent of fluid velocity. First let’s take a look at the general Bernoulli equation along a streamline.
(Eq 1) $p + \frac{1}{2}ρv^2+γh = C$
$p$ = thermodynamic pressure
$v$ = velocity
$ρ$ = density
$γ$ = specific weight
$h$ = fluid height
The first term $p$ represents the thermodynamic pressure of the flowing fluid. In order to measure this pressure you would have move at the same rate of the fluids flow and measure the static pressure that is relative to the flow. Another way to measure this pressure would be to use a piezometer tube. To use a piezometer tube you will need to drill a hole into the pipe that the fluid is flowing through, as seen in the image below.
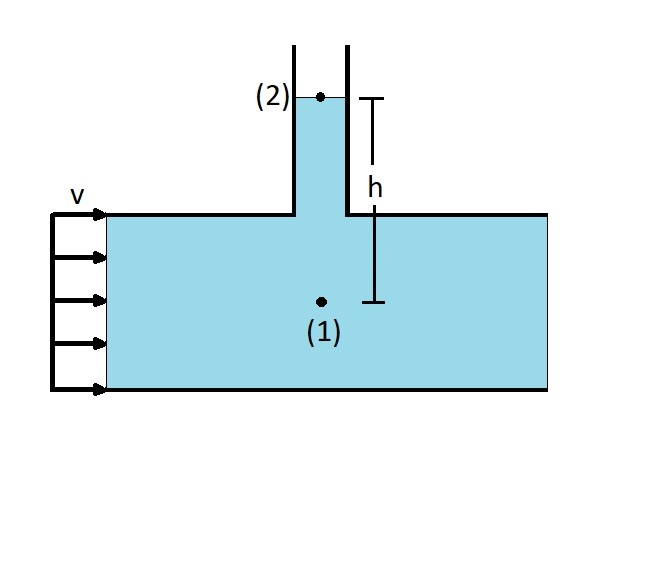
As the fluid flows past the piezometer the fluid will rise to a certain point. To find the thermodynamic pressure at point 1 you will need to use Bernoulli equation. Since the flow is perpendicular to the fluid flow, fluid velocity will not need to be considered on either side of the Bernoulli equation. Hence the image above can be represented by the following equation.
$p_1 = p_2 + γh_{2-1}$
Note, $p_2$ is atmospheric pressure. Since there is nothing stating that the pressure surrounding the pipe is at a different pressure than atmosphere $p_2$ will be cancelled out. Hence $p_1$ can be solved using the following equation.
$p_1 = γh_{2-1}$
You should notice that the above equation incorporates the third term of Bernoulli equation $γh$. This represents the hydrostatic pressure portion of Bernoulli equation. As a result both the first and third term of Bernoulli equation are static pressures.
Dynamic & Stagnation Pressure
The last part of the Bernoulli equation, the second term $\frac{1}{2}ρv^2$, represents the dynamic pressure. The dynamic pressure can be found by inserting a tube into the fluid flow where the tube opening is parallel to the flow. This can be seen in the image below. Once this has been done a stagnation pressure will develop at point 3 which is known as the stagnation point. To find the dynamic pressure you subtract the pressure at point 1 from the pressure at point 3.
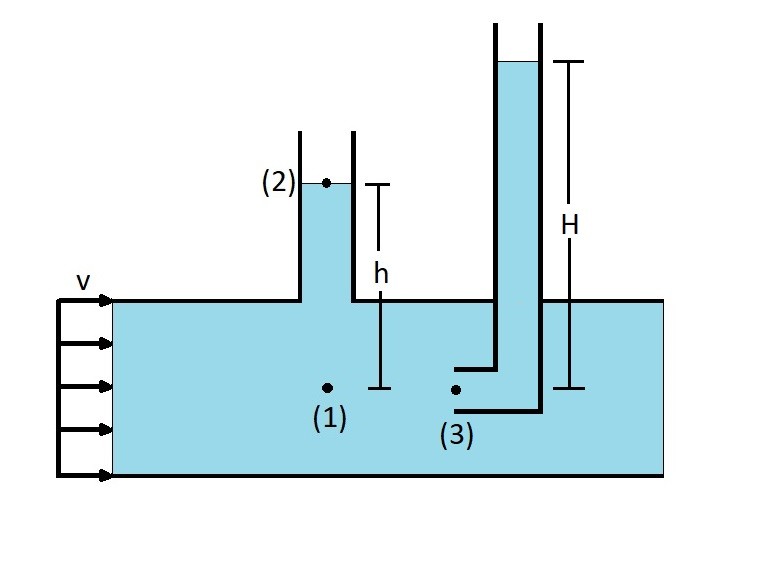
At the stagnation point the fluid velocity will go to zero. As a result Bernoulli equation can be used to determine what the stagnation pressure is at point 3 if you already know what the thermodynamic pressure is at point 1. Refer to the equation below.
$p_3 = p_1 + \frac{1}{2}ρv_1^2$
The stagnation pressure found at point 3 is largest pressure obtainable on a given streamline. The reason why is because it represents all of the kinetic energy within the fluid being converted into a hydrostic pressure rise represented by H.
Total Pressure
Finally, the total pressure is the sum of the thermodynamic pressure $p$, the dynamic pressure $\frac{1}{2}ρv^2$, and the hydrostatic pressure $γh$.