In a previous section I discussed forces along a streamline. However, in addition to forces along a streamline, there are also forces normal to a streamline.
Forces Normal to a Streamline
As a fluid particle move along a streamline forces will develop on the particle. As a result the free body diagram below represents the 2-dimensional forces on a particle. Be aware that I purposely didn’t include shear forces. When in reality there will always be some shear forces on a fluid particle due to viscous effects. On the particle in the diagram below the normal direction is represented by $\hat{n}$ while $\hat{s}$ represents the direction along the streamline.
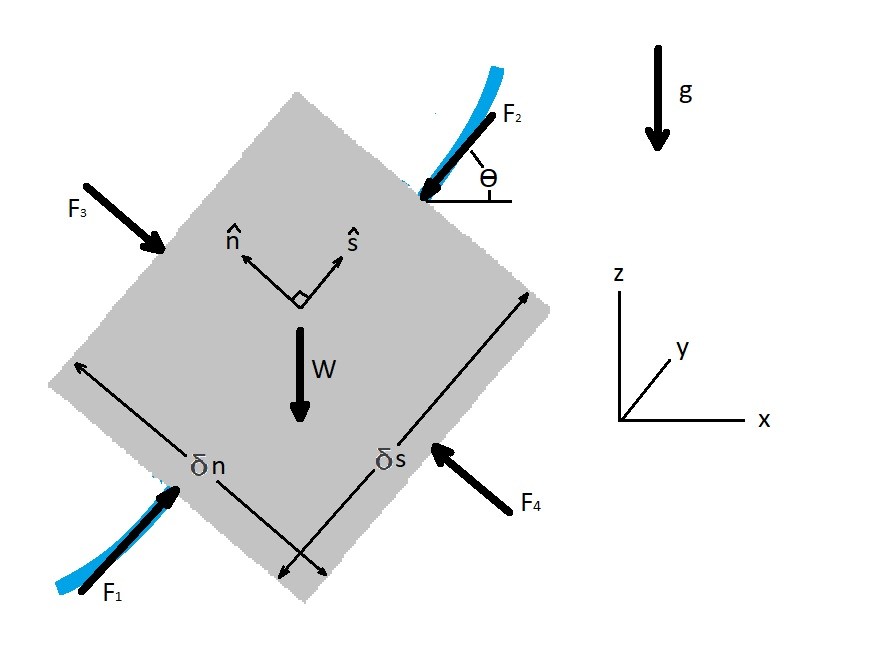
For the above diagram the forces in the normal direction can be described by the equations below.
(Eq 1) $\sum{}δF_n = δW_n+δF_{pn}$
where
$δW_n=-δWcosθ=-γδVcosθ$
and
$F_{pn} = F_4-F_3$$=(p-δp_n)δsδy-(p+δp_n)δsδy$ $=-2δp_nδsδy$$=-\frac{∂p}{∂n}δsδnδy$$=-\frac{∂p}{∂n}δV$
In addition to using the free body diagram to find the sum of the forces normal to the streamline, you can also use dynamics. To use dynamics you will need to know what the particles mass is, its current velocity, and the radius of the streamline. If you know these values you can calculate the normal force on the fluid particle using the following equation.
(Eq 2) $δF_n = \frac{δmv^2}{r}=\frac{ρδVv^2}{r}$
$δm$ = particle mass
$v$ = particle velocity
$r$ = streamline radius
$V$ = particle volume
$ρ$ = fluid density
Finally, if you were to allow $cosθ = \frac{dz}{dn}$ and than combine equations 1 and 2, the following equation will result.
(Eq 3) $-γ\frac{dz}{dn}-\frac{∂p}{∂n}=\frac{ρv^2}{r}$
The above equation is stating that to change the direction of flow there will need to be a combination of pressure gradient and particle weight that is normal to a streamline. Also, when there is large speed, or density, or a small streamline radius that would result in large force making the forces caused by gravity negligible, than equation 3 can be modified to the following.
(Eq 4) $\frac{∂p}{∂n}=-\frac{ρv^2}{r}$
Equation 4 would also be used when the flow is horizontal resulting in $\frac{dz}{dn}=0$.
Bernoulli Equation and Forces Normal to a Streamline
Now if we were to multiply equation 3 by $dn$, have $\frac{∂p}{∂n} = \frac{dp}{dn}$, and if the forces in the $\hat{s}$ direction are constant, we can integrate equation 3 to solve for a version of Bernoulli equation normal to the streamline.
(Eq 5) $\int{\frac{dp}{ρ} }+ \int{\frac{v^2}{r}dn}+gz = C$
$g$ = gravitation acceleration
$c$ = a constant that is based off of some point along the stream line
The above equation is used if the density of the fluid can change. In other words if the fluid compressible. If the fluid is incompressible, meaning that there is a constant fluid density, than equation 5 can be modified to the following.
(Eq 6) $p+ ρ\int{\frac{v^2}{r}dn}+γz = C$
As with Bernoulli equation for forces along a streamline, the assumption that you make are important. Hence, if you make the wrong assumption your results could be inaccurate.