If you were to look at a dam you might notice that there might be an area at the bottom of the dam where water is flowing out. What you are observing is a sluice gate. To calculate the flow through a sluice gate you will need to use a combination of Bernoulli equation and the continuity equation.
Recall that the general Bernoulli equation between two points along a streamline is the following.
(Eq 1) $p_1 + \frac{1}{2}ρv_1^2 + γz_1 = p_2 + \frac{1}{2}ρv_2^2+γz_2$
$p$ = thermodynamic pressure
$ρ$ = fluid density
$v$ = fluid velocity
$γ$ = specific weight
$z$ = fluid height
In order to use Bernoulli equation you will need to be able to make a few assumption. First, the flow must be inviscid. Next, the flow must be in a steady state. Finally, the fluid must be incompressible. If you cannot satisfy any of these assumptions, there will be inaccuracies in your results.
In addition to Bernoulli equation, you will also need to use the continuity equation to find the flowrate through a sluice gate. The equation below is the continuity equation for an incompressible fluid.
(Eq 2) $Q = A_1v_1 = A_2v_2$
$Q$ = flowrate
$A$ = cross-sectional area
Sluice Gate Flow Equation
As mentioned above to find the flow through a sluice gate you will need apply both Bernoulli and the continuity equation. First, lets take a look at a basic sketch of a sluice gate.
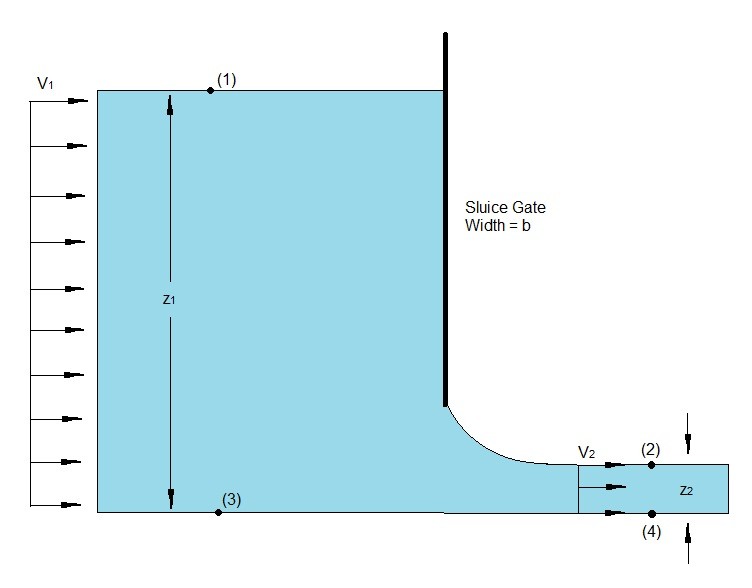
From the above sketch you should be able to see that the flow going through a sluice gate is dependent on the fluid height within the reservoir and the amount the sluice gate is open. So to start analyzing this problem we will need to look at points 1 and 2 on the above sketch.
First, let’s take a look at point 1. At point 1 we can say that the thermodynamic pressure is at atmosphere. The dynamic pressure is dependent on fluid velocity $v_1$. Finally, the hydraulic pressure is dependent on $z_1$.
Now we need to take a look at point 2. At point 2 the thermodynamic pressure is also at atmosphere. The dynamic pressure is dependent on the fluid velocity $v_2$. Finally, the hydraulic pressure is dependent on $z_2$.
From what is stated above we can cancel out the thermodynamic pressure on both sides of the equation since they are both at atmospheric pressure. Due to this the Bernoulli equation will become the following.
$\frac{1}{2}ρv_1^2 + γz_1 = \frac{1}{2}ρv_2^2+γz_2$
Next, we have to take a look at the continuity equation to define $v_1$ and $v_2$. This will result in the following.
$v_1 =\frac{Q}{A_1}=\frac{Q}{bz_1}$
$v_2 =\frac{Q}{A_2}=\frac{Q}{bz_2}$
Now that the $v_1$ and $v_2$ have been defined the above can be added to the Bernoulli equation.
$\frac{1}{2}ρ\left(\frac{Q}{bz_1}\right)^2 + γz_1 = \frac{1}{2}ρ\left(\frac{Q}{bz_2}\right)^2+γz_2$
Finally, we can solve the above equation for Q to find the flowrate through the sluice gate.
(Eq 3) $Q=z_2b\sqrt{\frac{2g(z_1-z_2)}{1-\left(\frac{z_2}{z_1}\right)^2}}$
$g$ = gravitational acceleration