The Bernoulli equation represents the energy equation of a fluid that is inviscid, incompressible, and at a steady flow along a streamline. As a result the hydraulic grade line and energy line can be found by using Bernoulli equation. To do this you will need have an understanding of what fluid head is. A fluids head is the total height that a fluid can reach due to its energy. To find the total head of a fluid you would have to divide Bernoulli equation by the specific weight of the fluid.
(Eq 1) $\frac{p}{γ}+\frac{v^2}{2g}+z=H$
$p$ = thermodynamic pressure
$γ$ = specific weight
$v$ = fluid velocity
$g$ = gravitational constant
$z$ = fluid height
$H$ = total head
Energy Line
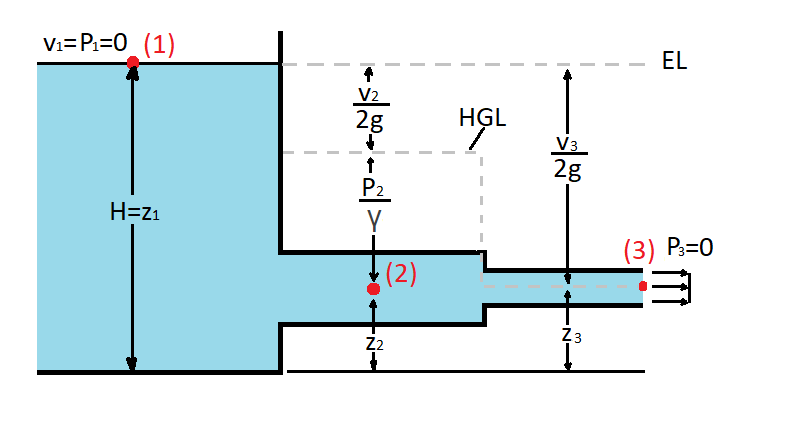
Now the question is what is the hydraulic grade line and energy line. Simply the hydraulic grade line and energy line represent a specific fluid head. First, let’s take a look at the energy line (EL). To determine the energy line you will need to find the total head of the system. This means that the energy line represents the maximum energy of the system. As a result this value will remain constant if all Bernoulli equation assumptions can be satisfied. For example what if the flow wasn’t inviscid. If this were the case than there would be energy losses due to a major head loss. The major head loss will cause the total head of the system to decrease as the fluid flows through the system. You can measure the total head at a point by measuring stagnation pressure.
Hydraulic Grade Line
The hydraulic grade line (HGL) on the other hand represents the fluid head caused by the thermodynamic pressure and hydrostatic pressure. Unlike the Energy line the hydraulic grade line can change even if all Bernoulli equation assumptions are met. It will change when the fluid velocity changes. As a result Hydraulic grade line can be calculated using the following equation. The hydraulic grade line can be determine by measuring the fluids static pressure using a piezometer tube.
(Eq 2) $HGL = H – \frac{v^2}{2g}= EL – \frac{v^2}{2g}$
The image below shows the hydraulic grade line and energy line of a fluid flowing out of a tank into atmosphere.