As a fluid particle moves along a streamline the particle will experience acceleration and deceleration. The resulting forces can be determine from Newton’s second law of motion.
(Eq 1) $F=ma$
$m$ = mass
$a$ = acceleration
For this article I will only be discussing the motion of inviscid fluids. By doing this I am saying that the viscosity of the fluid is zero. Which means there will be no frictional forces in the fluid as it flows. Be aware though that in real life there is no such thing as an inviscid fluid. However, in most cases the viscous forces of a fluid are so small that they can be considered negligible, though this may not always be the case.
When we are studying a fluid’s motion we assume that its motion will be governed by a pressure difference and gravitational forces. As a result Newton’s second law will apply to a fluid particle as seen in the following.
(Eq 2) (Net pressure force on a particle) + (net gravity force on a particle) = (particle mass) X (particle acceleration)
Streamlines and Newton’s Second Law
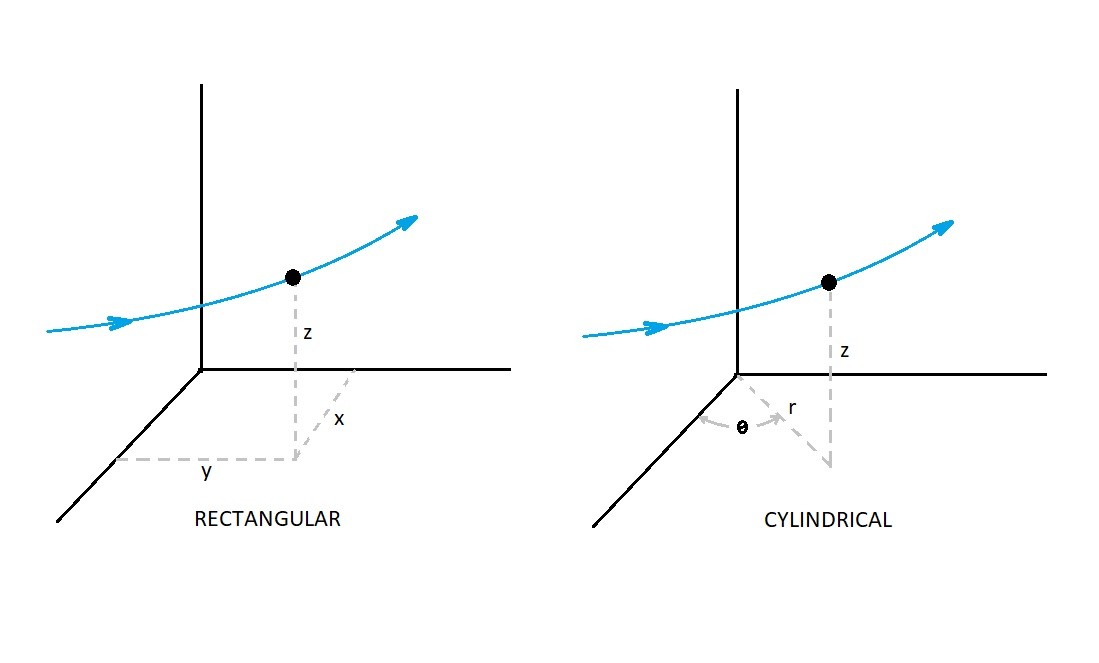
A streamline is the path that a fluid particle will take as it moves through a plumbing system or around an obstruction. To analyze a streamline you need to setup a coordinate system. This coordinate system can rectangular (x,y,z) or it could by cylindrical (r, θ, z). Determining the best coordinate system to use is dependent on what the flow geometry is. Below is an image showing the same streamline expressed in rectangular and cylindrical coordinates.
Generally a particles motion is defined in velocity along its streamline. From dynamics a velocity is defined by a change in position in relationship to time. Where the velocity is a vector quantity. This means that you will have to consider the velocity in all directions of the coordinate system that you chose. Finally, the total velocity of the particle will be the magnitude of the individual velocity quantities.
Now if the velocity was to change from one point to another an acceleration or deceleration will occur.
(Eq 3) $a_s=v\frac{∂v}{∂s}$
On the other hand a normal acceleration can occur when a particle is moving around a curve. Even if the velocity of the fluid particle on its streamline is constant, a normal acceleration will occur when the particle moves around a curve.
(Eq 4) $a_n=\frac{v^2}{r}$
$r$ = radius curve of particle streamline
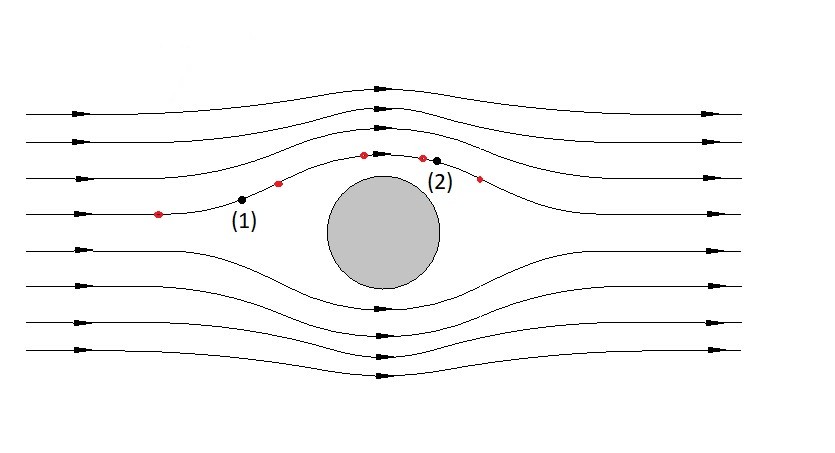
Finally, there can also be cases where there is steady flow. If steady flow is occurring than as particle move a long a certain stream line they will always pass through the same point. At the same time neighboring particles will follow their own paths, which can be different shape. This can be seen in the image below where all of the red particles will be passing through point 1 and point 2 on the streamline.