As fluid particle moves through space there will be forces along a streamline as well as forces that are normal to the streamline. The free body diagram of a fluid particle below shows both forces along a streamline as well as normal forces. Depending on how these forces balance can dictate how the particle will move. Which in essence will result in certain pressure on the particle as it moves to different parts of the streamline. For right now I am only going to focus on the forces along a streamline and omit the normal forces.
Recall that Newton’s second law states that $F=ma$. This equation can be rewritten to represent the forces along a streamline for a steady flow condition as seen below. This equation is valid for both compressible and incompressible fluids.
(Eq 1) $\sum{}F_s = δmv\frac{δv}{δs}=ρVv\frac{δv}{δs}$
$m$ = mass
$v$ = particle velocity
$δV=δsδnδy$ = particle volume
In addition to forces caused by the velocity change, which is represented by equation 1, you will also need to consider the weight of the particle. To determine how the weight would effect the particle along the streamline you would need to use the following equation.
(Eq 2) $W_s = -δWsinθ = -γδVsinθ$
$γ$ = specific weight
The only time equation two will not effect the forces along the stream line is if the streamline is horizontal. A horizontal streamline will result in θ equaling 0.
Fluid Particle Free Body Diagram
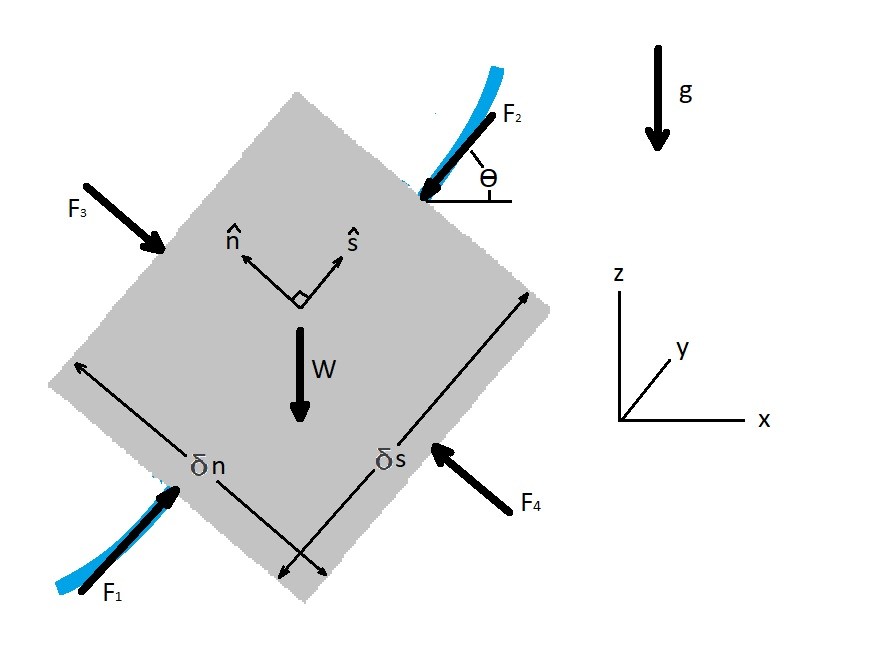
Above I have a fluid particle showing the 2-dimensional forces that can act on the particle. Be aware that I have purposely not included any shear forces on the particle. In reality there most likely would be shear forces on the particle due to viscous effects.
For the particle above $\hat{s}$ represents the direction along the streamline. On the other hand $\hat{n}$ represents the forces going in the normal direction. As mentioned above for right now I am going to ignore the normal forces. This means from the free body diagram the forces along the streamline can be represented by the equations below.
(Eq 3) $\sum{}δF_s=δW_s+δF_{ps}$
where
$δF_{ps} =F_1 – F_2$$=(p-δp_s)δ_nδy-(p+δp_s)δ_nδy = -\frac{δp}{δs}δV$
as a result
$\sum{}δF_s=\left(-γsinθ -\frac{δp}{δs} \right)δV$
Finally, the equation of motion caused by the forces along a streamline can be found by combining equation 1 and 3.
(Eq 4) $-γsinθ-\frac{δp}{δs}=ρv\frac{δv}{δs} = ρa_s$
$ρ$ = fluid density
$a_s$ = Fluid particle acceleration along streamline
Bernoulli Equation: Forces Along a Streamline
Now that the equation of motion has been defined we can now use that equation to define Bernoulli’s equation for forces along streamline. Before beginning you will need to have $sinθ=\frac{dz}{ds}$. In addition $v\frac{dv}{ds}=\frac{1}{2}\frac{dv^2}{ds}$. Finally, your normal forces (n) is constant $dn = 0$. By having $dn = 0$ you will be able to define $dp = \left(\frac{∂p}{δs}\right)ds +\left(\frac{∂p}{δn}\right)dn = \left(\frac{∂p}{δs}\right)ds $. As a result $p(s,n) = p(s)$ and $ \frac{∂p}{∂s} = \frac{dp}{ds}$. Taking all of this into consideration equation 4 can be modified to the following.
(Eq 5) $-γ\frac{dz}{ds}-\frac{dp}{ds} = \frac{1}{2}ρ\frac{dv^2}{ds}$
or
$dp+\frac{1}{2}ρdv^2+γdz = 0$
Next since gravitational acceleration is constant the above equation can be integrated to the following equation.
(Eq 6) $\int{\frac{dp}{ρ}}+\frac{1}{2}v^2+gz = C$
$C$ = a constant that is based of some point along the streamline
Now notice that the pressure was not integrated for the equation above. The reason for this is because in general the pressure cannot be integrated since the density may not be constant if the fluid is compressible. If the fluid is compressible, meaning the density can change, than you will need to use the ideal gas law. On the other hand if you know the fluid is incompressible, which is a good assumption for a liquid, than equation 6 can be modified to the following equation.
(Eq 7) $p+ \frac{1}{2}ρv^2+γz = C$
Bernoulli Equation Assumptions
Notice that equation 7 is Bernoulli equation. The Bernoulli equation is very powerful tool in fluid mechanics. This is due to the fact that it will allow you to determine changes in fluid pressure or fluid velocity from one point to another point along a streamline. However, when using Bernoulli’s equation you have to make the following assumptions. First, the viscous effects must be negligible. Second, the flow must be in a steady state. Third, the fluid is incompressible. Fourth, you are analyzing flow along a streamline not normal to the streamline. If any of these assumptions are bad assumptions for the particular problem that you are looking at, than there will inaccuracies in your result.