Have you ever wondered how an airplane measures its airspeed. One way it does this is by using Pitot-static tubes, or pitot tube for short. A pitot tube is a device that measures static pressure as well as stagnation pressure. By measuring both types of pressure the pitot tube can determine speed of a fluid, or the speed of an object, such as a plane, moving through the fluid.
Static and Stagnation Pressure
Briefly let me remind you what static and stagnation pressure are. First let’s take a look at Bernoulli equation for forces along a streamline.
(Eq 1) $p + \frac{1}{2}ρv^2 + γh = C$
$p$ = thermodynamic pressure
$ρ$ = fluid density
$v$ = fluid velocity
$γ$ = specific weight
$h$ = fluid height
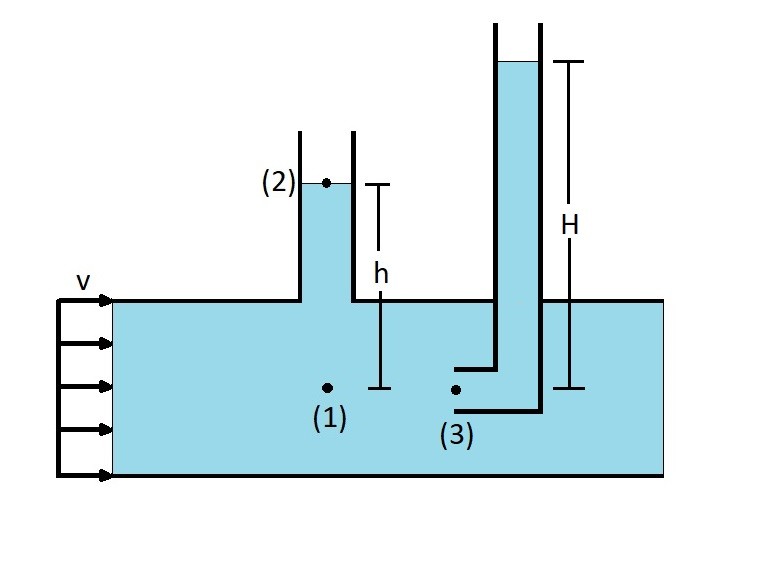
A static pressure is a fluid pressure that is independent of fluid velocity. As a result the first part $p$ and the third part $γh$ are both static pressures. Where $γh$ is the hydrostatic pressure. In the figure below the thermodynamic pressure at point 1 can be determine by the fluid height at point 2 by using the following modification of Bernoulli equation.
$p_1 = γh$ (this is a static pressure)
The stagnation pressure on the other hand represents all of the kinetic energy that has been converted into a pressure rise represented by H is the figure below. As a result the stagnation pressure is found at point 3. To obtain the stagnation pressure the opening of the tube has to be perpendicular to the fluid flow.
$p_3 = p_1 +\frac{1}{2}ρv^2$
Pitot Tubes
A Pitot tube works by measuring both static pressure as well as the stagnation pressure of an air flow. Once these values are found the fluid velocity can be found. This can be seen in the equation below by rearranging the terms used to find the stagnation pressure for image above.
(Eq 2) $v=\sqrt{2(p_3-p_1)/ρ}$
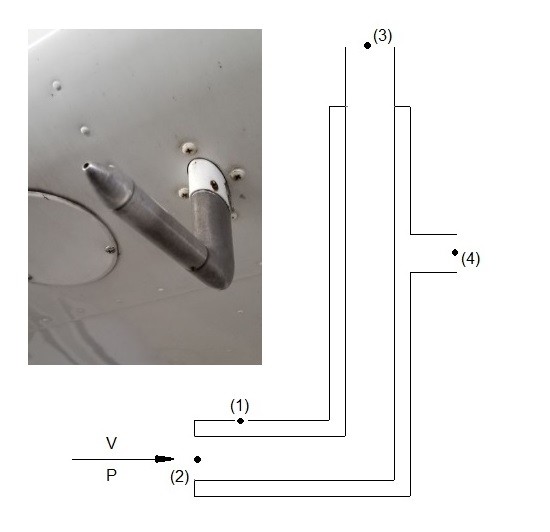
Below is an image of an actual pitot tube on an aircraft, with a basic diagram showing how it would work. As the aircraft is flying static pressure will develop at point 1 and 4. As along the difference in height is negligible the pressure at point 1 and 4 can be considered the same.
$p_4 =p_1 =p$
Next, a stagnation pressure will develop at point 3 as the aircraft move through the air.
$p_3 =p_4+ \frac{1}{2}γv^2$
As result the velocity of the aircraft can be determine by the following equation.
$v=\sqrt{2(p_3-p_4)/ρ}$
Due to its simplicity, the pitot tube is an inexpensive way of measuring fluid speed. However, if not done correctly, inaccuracies can result. First, to measure static pressure, non of the fluid kinetic pressure can be converted in a pressure rise. In other words the openings in the tube that measure static pressure must be perpendicular to the fluids flow. You also want to make sure there are no imperfections in or on the holes that are measuring static pressure. In addition, to measure the stagnation pressure correctly, the opening of the tube needs to be parallel with the fluid flow. Generally, it can be difficult to perfectly align a pitot tube so that it is directly the direction of the flow. One way to solve this issue is to use a directional-finding pitot tube. Refer to the image below.
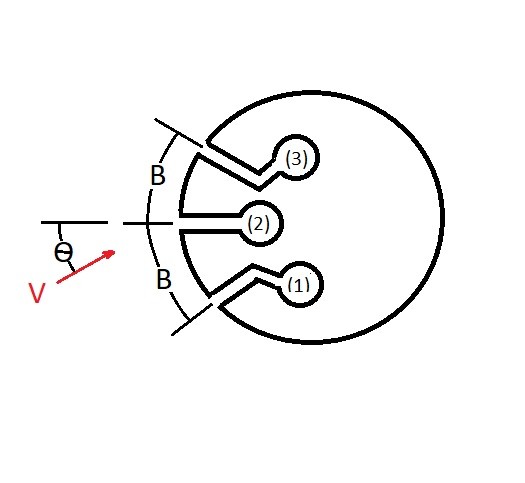
The way a directional finding pitot tube works is it uses two side holes, represented by 1 and 3 in figure above. When these two holes have have an equal pressure, than hole 2 is oriented into the fluid stream. If holes 1 and 3 do not have an equal pressure the pitot tube needs to be adjusted.