The Bernoulli Equation. This equation is probably one of the most important equations that you will use in fluid mechanics. The reason why is because it is capable of relating fluids velocity to a pressure change between to two points. As a result most fluid mechanics problems will use a form of this equation.
What is Bernoulli Equation?
As stated above the Bernoulli equation main use is to relate a fluids pressure to it velocity. To be more technical, by the Bernoulli principle “an increase in the speed of a fluid occurs simultaneously with a decrease in pressure.” As stated by Daniel Bernoulli.
So why is Bernoulli equation so important? The answer to this is quite simple. The Bernoulli equation allows us to describe a fluids characteristics from one point of a streamline to another point of streamline. It does this by taking in consideration of the thermodynamic pressure ($p$), the dynamic pressure, ($\frac{1}{2}ρv^2$), and the hydrostatic pressure ($γh$). In the end the general Bernoulli equation between two points will look like the following equation.
(Eq 1) $p_1+\frac{1}{2}ρv_1^2+γz_1 = p_2+\frac{1}{2}ρv_2^2+γz_2$
$p$ = Thermodynamic Pressure
$ρ$ = fluid density
$v$ = fluid velocity
$γ$ = specific weight
$z$ = fluid height
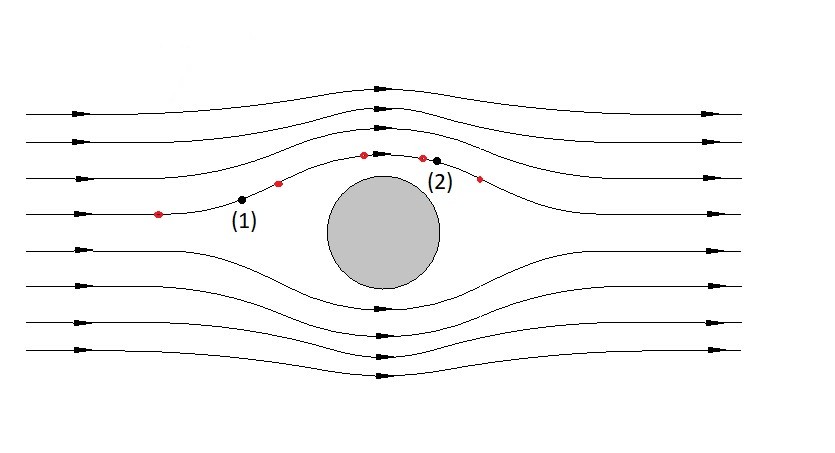
Applications of Bernoulli Equation
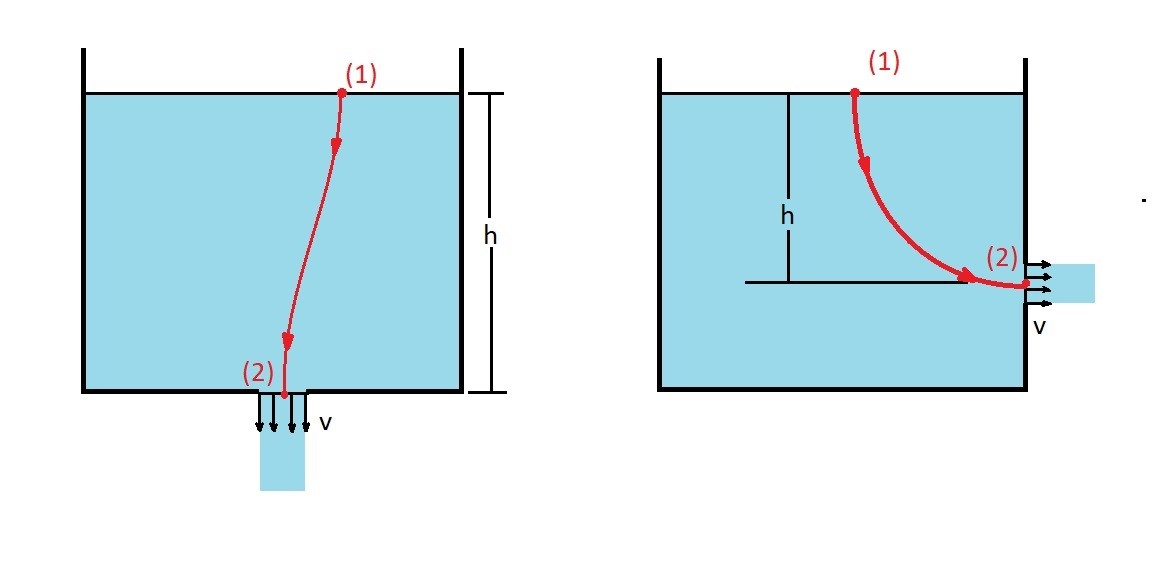
So what are some application of Bernoulli equations. The first common application of Bernoulli equation would be studying free jets. Free jets occur when there is a small hole in a reservoir that allows fluid to escape. As the fluid flows out of the hole a jet of fluid will result. This can be seen in the images below.
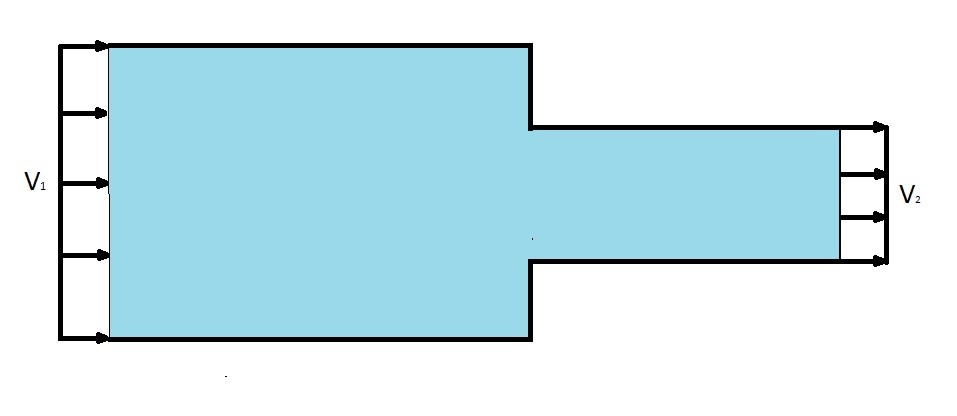
The Bernoulli equation can also be used to solve confined flow problems where the diameter of piping changes. Refer to the image below.
These are just a couple example of the type of problems Bernoulli equation can analyze. There are many more.
Bernoulli Equation Assumptions
When you are using Bernoulli equation you will need to make some assumptions. The assumptions are as follows. First, you must assume that viscous effects are negligible. Second, the flow must be in a steady state condition. Third, the fluid has to be incompressible. Finally, fourth, the above equation is only applicable for studying fluid flow along a streamline. If you cannot reasonably make these assumption than you will need to use modified versions of the Bernoulli equation. Otherwise your result will be inaccurate.