Head loss is a loss in pressure head due to the viscosity of a fluid and obstructions to a fluid such as pipe elbows, valves, etc. By knowing the head loss, you can successfully modify Bernoulli’s energy equation accordingly; refer to equation 1. Bernoull’s energy equation is Bernoulli’s equation divided by the fluid’s specific weight.
(Eq 1) $\frac{P_1}{γ}+α_1\frac{v_1^2}{2g}+z_1=\frac{P_2}{γ}+α_2\frac{v_2^2}{2g}+z_2+h_L$
P = Pressure
γ = Specific Weight
α = Energy Coefficient
v = Velocity
g = Gravitational Constant
z = Fluid Height
HL = Head Loss
In equation 1 α represents the energy coefficient. The energy coefficient is 1 when the flow is developed. However, if the flow is undeveloped the energy coefficient will be less than 1. Finally, hl represents the head loss.
There are two different types of head losses that make up the total head loss seen in equation 2. These head losses are the major head loss and the minor head loss.
(Eq 2) $h_L=h_{L_{major}}+h_{L_{minor}}$
Major Head Loss
The major head loss considers the drop in pressure due to viscous effects. To calculate the major head loss equation 3 would be used.
(Eq 3) $h_{L_{major}}=f\frac{L}{D}\frac{v^2}{2g}$
hLmajor = Major Head Loss
f = Friction Factor
L = Pipe Length
D = Pipe Diameter
v = Fluid Velocity
g = Gravitational Constant
The variable f in equation 3 represents the friction factor. To calculate the friction factor for laminar flow equation 4 would be used. If the flow is turbulent then the Moody Chart could be used, or equation 5 could be used.
(Eq 4) $f=\frac{64}{Re}$
Re = Reynolds Number
(Eq 5) $\frac{1}{\sqrt{f}}-2.0·log\left(\frac{ε/D}{3.7}+\frac{2.51}{Re·\sqrt{f}}\right)$
Moody Chart (source Wikipedia )
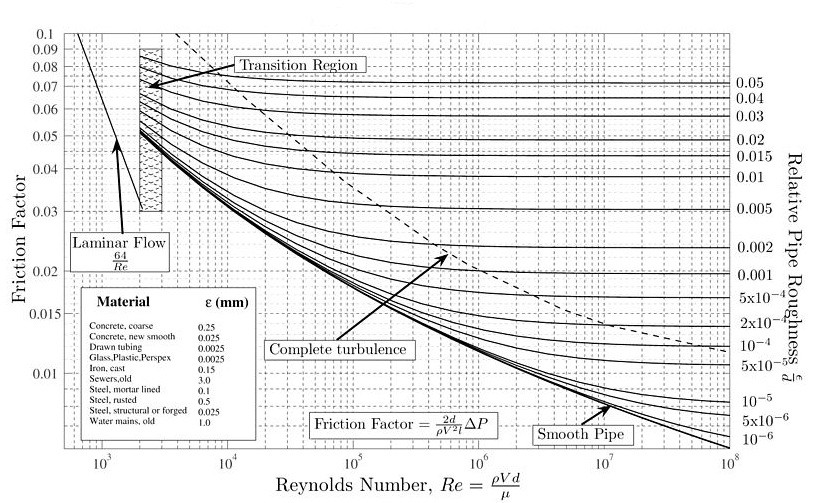
From equation 5, ε represents the roughness of the pipe’s surface. The roughness of the pipe’s surface has little to no effect on laminar flow.
Minor Head Loss
Minor head loss is due to any pressure drop caused by an elbow, tee, valve, etc. To calculate the minor head loss equation 6 would be used.
(Eq 6) $h_{L_{minor}}=k_L\frac{v^2}{2g}$
hLminor = Minor Head Loss
kL = Minor Head Loss Coefficient
v = velocity
g = gravitational constant
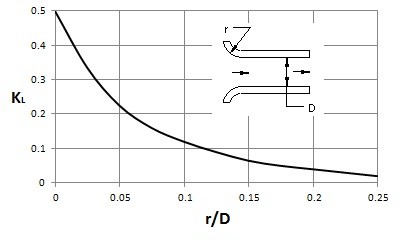
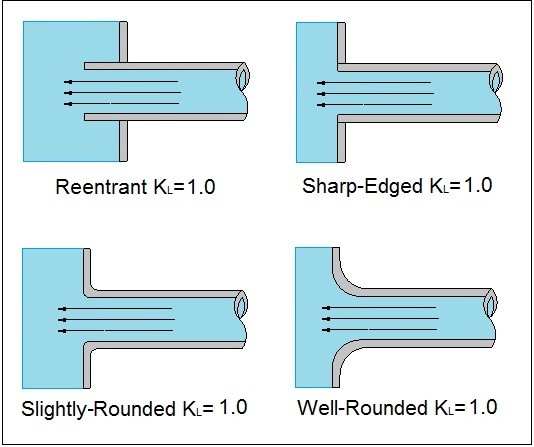
The coefficient kL in equation 6 represents the loss coefficient. To determine the loss coefficient for various situations refer to the tables and images below.
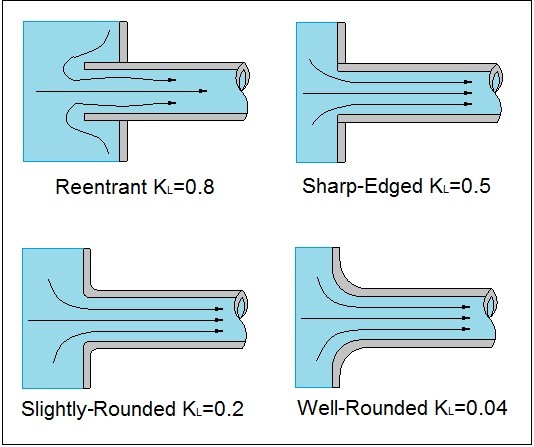
Minor Head Loss Pipe Entrance
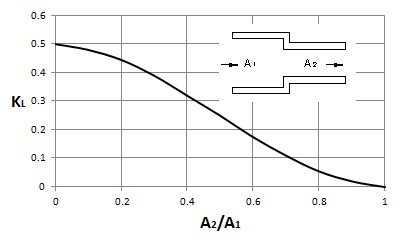
Minor Head Loss Pipe Exit
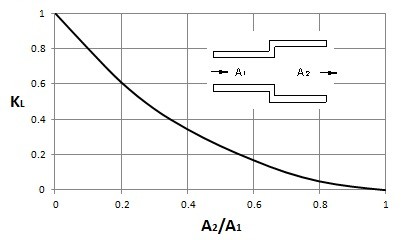
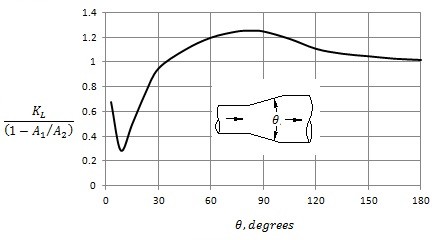
Minor Head Loss Conical Diffuser
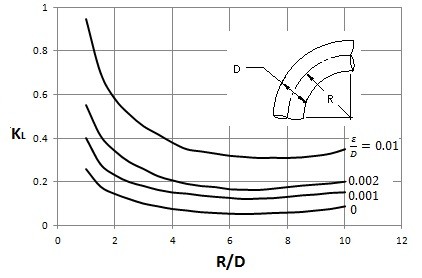
Minor Head Loss 90 Degree Bend