Bernoulli equation can be used to study a free jet as the a fluid leaves a large reservoir. First, recall that in order to use Bernoulli equation you will need to pick 2 points on a stream line. However, at those points you will need to make a few assumptions. First, the flow must be steady. Second, the fluid must be inviscid. Finally, the fluid must be incompressible. If these are poor assumptions for the problem you are analyzing inaccuracies will result. Below is a general example how the Bernoulli’s equation should be setup.
(Eq 1) $p_1+\frac{1}{2}ρv_1^2+γz_1 = p_2 +\frac{1}{2}ρv_2^2+γz_2$
$p$ = thermodynamic pressure
$ρ$ = fluid density
$v$ = fluid velocity
$γ$ = specific weight
$z$ = fluid height
You should notice that there are 6 unknown variables in the above equation. They are thermodynamic pressure, fluid velocity, and fluid height at the two points chosen on the streamline. As a result in order for you to use Bernoulli’s equation you will need know five of these six unknowns.
Free Jets
Let’s get back to talking about free jets. First what is a free jet? A free jet is created when there is a small opening in a large reservoir that goes to atmosphere. A free jet can occur on the bottom of the container, or the side of the container. Where ever it occurs though, Bernoulli equation can be used to describe its characteristics.
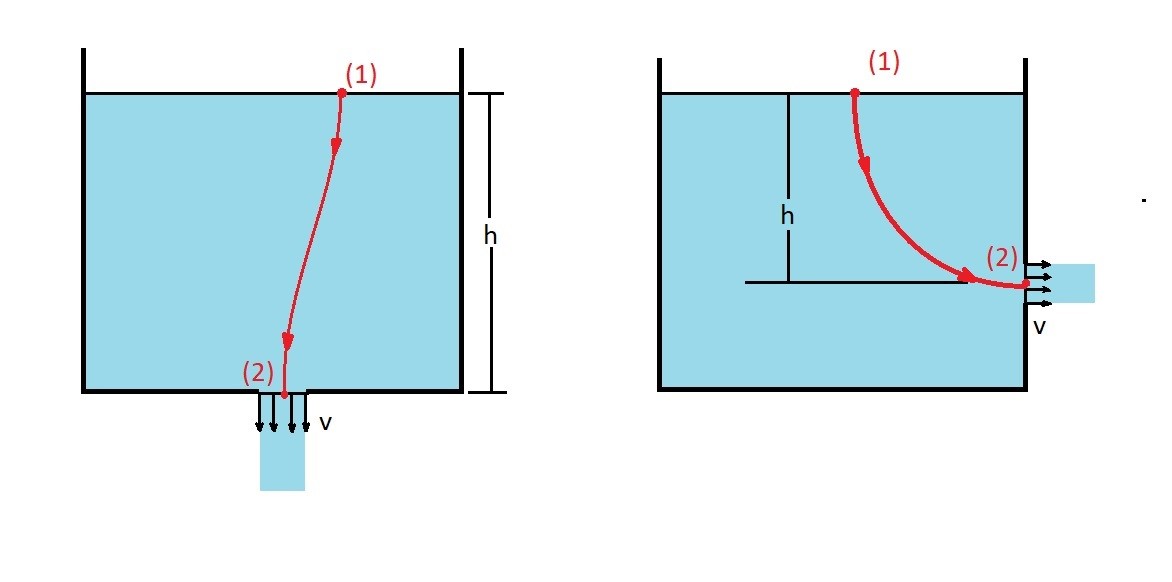
Let’s take a look at the above image. Here I am showing two cases where there is free jet present. The first case is that there is a free jet leaving the bottom of a reservoir. On the other hand the second case shows a free jet leaving through the side of the reservoir. Even though they look like two completely different problems they are not. They are actually the same problem.
First, let’s take a look a point 1. At point 1 for both cases the thermodynamic pressure is going to be at atmosphere. In addition the fluid height $z_1$ is at a distance of h from point 2. Finally, we can assume that the reservoirs are significantly large enough that there will be negligible fluid velocity at point 1. Hence the 3 unknowns are as follows.
$p_1$ = atmospheric pressure
$v_1$ = 0
$z_1$ = h
Now let’s take a look at point 2. As with point 1 the thermodynamics pressure will be at atmosphere at point 2. In addition, $z_2$ is distance of h from point 1. However, since this will not cause a hydrostatic pressure on point 1 $z_2$ will equal zero. Finally, there is a velocity $v$ at point 2. As a result the 3 unknowns at point 2 are the following.
$p_2$ = atmospheric pressure
$v_2$ = v
$z_2$ = 0
You should notice that $p_1 = p_2$. Due to this fact those terms will cancel out. Now that all of the terms have been defined we can write an equation that will describe the characteristics of a free jet.
(Eq 2) $γh = \frac{1}{2}ρv^2$
This equation is used to describe both cases in the image above. It can also be use to describe characteristic of a water fountain seen the image below. Where point 1 will be at the top of the water jet, and point 2 will be at the point where the water jet comes out of the nozzle.
