Determining the momentum on fluid element will allow you to determine the forces and corresponding pressures on the fluid element. Generally, the easiest method is to use a finite control volume. However, sometimes you may require more detail in your results. As a result you will need to use the differential momentum equation instead.
First, to derive the differential momentum equation you will need to look at the linear momentum equation.
(Eq 1) $F=\frac{DP}{Dt}$
$F$ = resultant force
$P$ = linear momentum $P=\int_{sys}vdm$
$D(~)/Dt$ = material derivative
If you are using a finite control volume, and you are only interested in what is occurring on the control surface, than you can use the following linear momentum equation.
(Eq 2) $\sum{F}_{CV} = \frac{∂}{∂t}\int{_{CV}}vρdV+\int{_{CS}}vρv·\hat{n}dA$
However, if you want to know more about how the fluid is behaving within the control volume, than you will need to apply the differential momentum equation. To do this you will need to analyze an infinitesimal control volume $δV$. That infinitesimal control volume will have a mass $δm$. Hence, by using this approach the linear momentum equation will become the following.
(Eq 3) $δF = \frac{D(vδm)}{Dt}$
or
$δF = δm\frac{Dv}{Dt}$
In the above equation $Dv/Dt$ represents acceleration $a$. In turn, equation 3 can be modified to the following equation.
(Eq 4) $δF = δma$
Notice that equation 4 is Newton’s second law applied to $δm$.
Forces Acting on a Differential Element
There are two type of forces that can act on a fluid element. First, surface forces can act on the fluid element. Surface forces are forces that interact only with the surface of the fluid element. Next, body forces can act on the fluid element. In contrast to surface forces, body forces distribute throughout the entire element. An example of a body force would be the weight $δF_b$ of the element.
(Eq 5) $δF_b=δmg$
$g$=gravitational acceleration
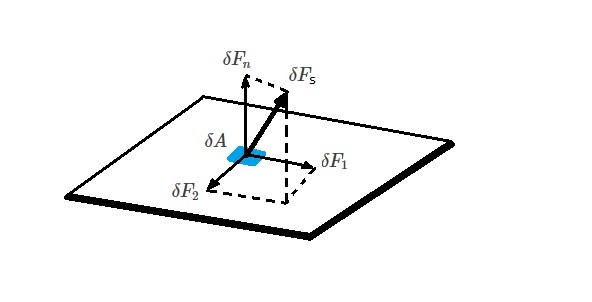
Besides the weight of the fluid element, most forces acting on the fluid element will be surface forces caused by its interactions with its surroundings. In turn, these forces can cause normal and shear stresses depending how the force interacts with the arbitrary surface area δA. Hence, if the force is normal to the surface area a normal stress will result.
(Eq 6) $σ_n=lim_{δA→0}~\frac{δF_n}{δA}$
In addition, there are the forces $δF_1$ and $δF_2$ that are parallel to the surface of the element. As a result, these type of forces will cause a shear force to develop on the surface of the element.
(Eq 7) $τ_1=lim_{δA→0}\frac{δF_1}{δA}$
(Eq 8) $τ_2=lim_{δA→0}\frac{δF_2}{δA}$
Generally, it is convenient to reference a coordinate system when discussing stresses. For example, if we were analyzing stresses that are on the yz plane, than the normal stress will be $σ_{xx}$ and the two shear forces will be $τ_{xy}$ and $τ_{xz}$. In turn, this will allow us to easily identify the particular stress component. This is due to the fact that the first subscript is the coordinate that is normal to the plane of interest. On the other hand, the second subscript is the direction of the stress.
Finally, the surface stress on each face of the element cube can be determine by using a Taylor series expansion. Hence the stress in the x-direction will yield the following equation.
(Eq 9) $δF_{sx}=\left(\frac{∂σ_{xx}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}\right)δxδyδz$
In addition, you can apply this to the y and z directions.
(Eq 10) $δF_{sy}=\left(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_{yy}}{∂y}+\frac{∂τ_{zy}}{∂z}\right)δxδyδz$
(Eq 11) $δF_{sz}=\left(\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y}+\frac{∂σ_{zz}}{∂z}\right)δxδyδz$
Finally, the resultant surface force can be found by combining equations 9-11.
(Eq 12) $δF_s=δF_{sx}\hat{i}+δF_{sy}\hat{j}+δF_{sz}\hat{k}$
Once the resultant surface force is combined with the resultant body force the total force acting on the differential mass can be determined.
(Eq 13) $δF=δF_s+δF_b$
Equation of Motion
In order to determine the equations of motion, the body and surface forces will need to be combined with equation 4. However, in order to do this equation 4 will need to be broken down into its x, y, and z components.
(Eq 14) $δF_x=δma_x$
(Eq 15) $δF_y=δma_y$
(Eq 16) $δF_z=δma_z$
Next, $δm=ρδxδyδz. Hence,
(Eq 17) $ρg_x+\frac{∂σ_{xx}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z} = ρ\left(\frac{∂u}{∂t}+u\frac{∂u}{∂x}+ν\frac{∂u}{∂y}+w\frac{∂u}{∂z}\right)$
(Eq 18) $ρg_y+\frac{∂τ_{xy}}{∂x}+\frac{∂σ_{yy}}{∂y}+\frac{∂τ_{zy}}{∂z} = ρ\left(\frac{∂ν}{∂t}+u\frac{∂ν}{∂x}+ν\frac{∂ν}{∂y}+w\frac{∂ν}{∂z}\right)$
(Eq 17) $ρg_z+\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y}+\frac{∂σ_{zz}}{∂z} = ρ\left(\frac{∂w}{∂t}+u\frac{∂w}{∂x}+ν\frac{∂w}{∂y}+w\frac{∂w}{∂z}\right)$
Finally, the above equations are general equations of motion. Due this, they can be used for both solids and fluids. However, before they can be used, additional information about the stresses will need to be gathered for the specific problem of interest. Otherwise, there will be more unknowns than available equations.