To use Newton’s second law you will need derive an acceleration field. You can use the Lagrangian method to define the acceleration field. By using the Lagrangian method you will track individual fluid particles. You can do this by using the material derivative.
First, let’s talk about acceleration. So when does fluid particle Acceleration occur? One way that fluid acceleration will occur is when the flow is unsteady. As result the fluid velocity at a given point will vary with time. Acceleration of fluid particle will also occur when the fluid velocity changes do a change in cross-sectional area. This type of acceleration will occur for both steady and unsteady states of flow.
The Material Derivative
Now let’s talk about the material derivative. To derive the material derivative you will first need to consider a fluid particle that is moving along a pathline. Refer to the image below.
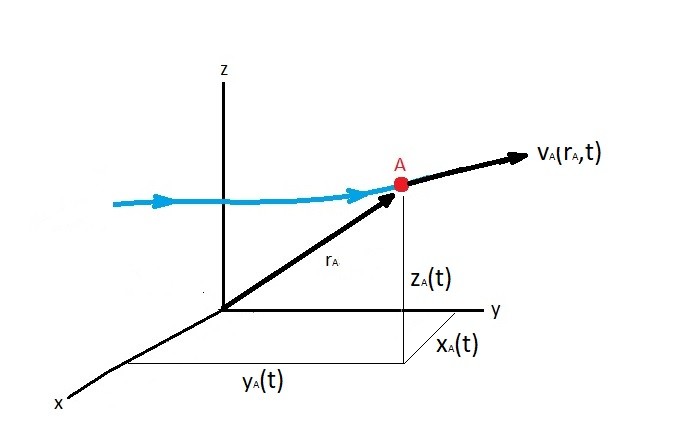
Let’s take a look at particle A’s velocity ($v_A$). The particle velocity will be both a function of time and location.
(Eq 1) $v_A=v_A(r_A,t)=v_A[x_A(t), y_A(t), z_A(t),t]$
To define acceleration you would need define the velocities rate of change in respect to time. However, as stated above, the velocity of a particle is both a function of time and location. As a result, to derive the acceleration equation from equation 1 you will need to use the chain rule.
(Eq 2) $a_A(t)=\frac{dv_A}{dt}=\frac{∂v_A}{dt}+\frac{∂v_A}{∂x}\frac{dx_A}{dt}+\frac{∂v_A}{∂y}\frac{dy_A}{dt}+\frac{∂v_A}{∂z}\frac{dz_A}{dt}$
Equation 2 can be simplified by defining the velocity components in the following manner. $u_a = dx_A/dt$, $ν_A=dy_A/dt$, and $w_A=dz_A/dt$.
$a_A = \frac{∂v_A}{∂t}+u_A\frac{∂v_A}{∂x}+ν_A\frac{∂v_A}{∂y}+w_A\frac{∂v_A}{∂z}$
The above equation will apply to all fluid particles. As a result the subscript A can be removed from the equation. This will result in equation 3.
(Eq 3) $a= \frac{∂v}{∂t}+u\frac{∂v}{∂x}+ν\frac{∂v}{∂y}+w\frac{∂v}{∂z}$
Equation 3 represent the vector equation of for the acceleration of a fluid particle. This can be broken into the following scalar equations to obtain the acceleration of the fluid particle in the x, y, and z directions.
$a_x=\frac{∂u}{∂t}+u\frac{∂u}{∂x}+ν\frac{∂u}{∂y}+w\frac{∂u}{∂z}$
$a_y=\frac{∂ν}{∂t}+u\frac{∂ν}{∂x}+ν\frac{∂ν}{∂y}+w\frac{∂ν}{∂z}$
$a_z=\frac{∂w}{∂t}+u\frac{∂w}{∂x}+ν\frac{∂w}{∂y}+w\frac{∂w}{∂z}$
Finally, the above the equations can be written in short hand notation.
$a=\frac{Dv}{Dt}$
where the operator is
(Eq 4) $\frac{D(~)}{Dt}≡\frac{∂(~)}{∂t}+u\frac{∂(~)}{∂x}+ν\frac{∂(~)}{∂y}+w\frac{∂(~)}{∂z}$
Equation 4 represent the material derivative. Often the material derivative will be written in shorthand notation, as seen in the equation below.
(Eq 5) $\frac{D(~)}{Dt}=\frac{∂(~)}{∂t}+(V·∇)(~)$
The material derivative can be used for multiple fluid parameters not just acceleration. For example what if you wanted to use the material derivative for temperature where $T = T(x,y,z,t). If that were the case than the material derivative would become the following equation.
$\frac{D(T)}{Dt}=\frac{∂(T)}{∂t}+(V·∇)(T)$
Unsteady Effects
There are two parts of material derivative, the time derivative $∂(~)/∂t$ and the spatial derivatives $∂(~)/∂x$, $∂(~)/∂y$, and $∂(~)/∂z$. The time derivative is a local derivative which represents local acceleration $∂v/∂t$. If the flow is steady the time derivative will equal zero through out the flow field since any local effects from local acceleration will cancel out. As a result there will be no change in flow at any point in the flow field. On the other hand when you have unsteady flow other fluid parameters such as temperature and density can change at any location in respect to time.
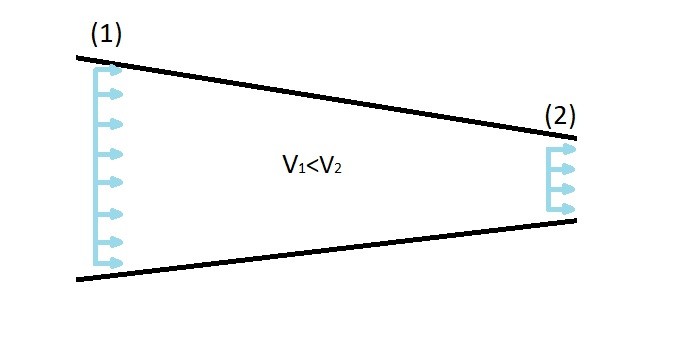
Convective Effects
Again as mention above the material derivative has two parts, the time derivative and the spatial derivatives. While the time derivative represents local acceleration, the spatial derivative represents the convective effects. As a result the spatial derivatives are also called the convective derivatives. The convective derivatives represents the fact that the flow properties from one point to another point can change. An example of this would be a fluid flowing through a nozzle. As the fluid flows through the nozzle its velocity will increase as the diameter of the nozzle decreases. Hence an acceleration occurs on the fluid particles regardless of whether the flow is steady or unsteady. As a result convective acceleration occurs due to a change in geometry.