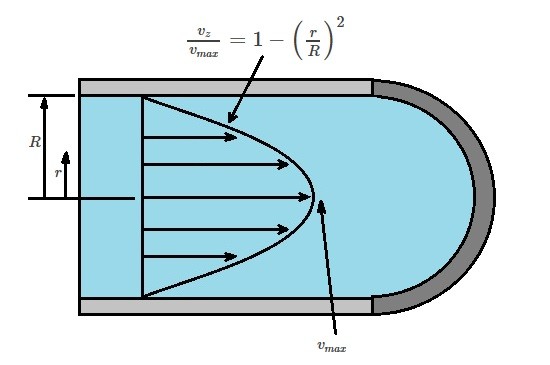
Another application of the Navier-Stokes Equations is for steady state, incompressible flow through a straight circular tube that has a constant cross section. For this article we will be considering a horizontal tube with a radius $R$. In addition, we will also assume that the velocities of the flow parallel to the walls will be $v_r=0$ and $v_θ=0$. Another condition that will be applied is $∂v_z/∂z=0$ due to the continuity equation. Finally, $v_z$ is not a function $θ$ or $t$. As a result, the velocity $v_z$ will only be a function of the radial position $v_z=v_z(r). Taking all of these conditions into consideration the Navier-Stokes equation become the following for laminar flow through a circular tube.
(Eq 1) $0=-ρg~sin~θ-\frac{∂p}{∂r}$
(Eq 2) $0=-ρg~cos~θ-\frac{1}{r}\frac{∂p}{∂θ}$
(Eq 3) $0=-\frac{∂p}{∂z}+μ\left[\frac{1}{r}\frac{∂}{∂r}\left(r\frac{∂v_z}{∂r}\right)\right]$
If $θ$ is measured from the horizontal plane, gravity will have the following effect on the fluid; $g_r=-g~sin~θ$ and $g_θ=-g~cos~θ$. Taking gravity into consideration, equations 1 and 2 can be combined and integrated to derive a function to calculate pressure $p$ due to gravitational effects.
(Eq 4) $p=ρg(r~sin~θ)+f_1(z)=-ρgy+f_1(z)$
The function above shows the pressure will be hydrostatically distributed. It also shows that the pressure gradient, $∂p/∂z$, is not function of the radius $r$ or the angle $θ$.
Equation 3 represents the equation of motion. It can also be written in the following form.
(Eq 5) $\frac{1}{r}\frac{∂}{∂r}\left(r\frac{∂v_z}{∂r}\right)=\frac{1}{μ}\frac{∂p}{∂z}$
Next, we will integrate equation 5 twice to derive the velocity function.
First Integration:
(Eq 6) $r\frac{∂v_z}{∂r}=\frac{1}{2μ}\left(\frac{∂p}{∂z}\right)r^2+c_1$
Second Integration:
(Eq 7) $v_z=\frac{1}{4μ}\left(\frac{∂p}{∂z}\right)r^2+c_1~ln~r+c_2$
Next, to fully define the velocity function the constants $c_1$ and $c_2$ need to be determined. They are found by defining a set of boundary conditions. In this case $v_z$ will be finite at the center of the tube ($r=0$). In addition, at the tube wall ($r=R$) fluid velocity will zero. Hence, when $ln(0)=-∞$ $c_1=0$. Due to this fact, $c_2$ is defined as the following equation.
(Eq 8) $c_2=-\frac{1}{4μ}\left(\frac{∂p}{∂z}\right)R^2$
As a result, the velocity function becomes the following.
(Eq 9) $v_z=\frac{1}{4μ}\left(\frac{∂p}{∂x}\right)(r^2-R^2)$
From equation 9 it can be seen the velocity distribution is parabolic.
Volume Rate of Flow
Next, let’s take a look at the volume flow rate and how it relates to the pressure gradient. In order to determine volume flow rate through a circular tube you will need to analyze a washer shaped ring taken from the cross-section of the tube.
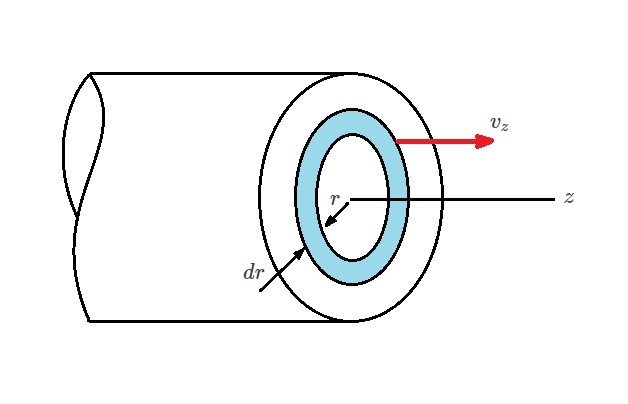
The velocity $v_z$ is constant within in the ring. In addition, the differential $da=(2πr)dr$. In turn, the following equation will result.
(Eq 10) $dQ=v_z(2πr)dr$
or
(Eq 11) $Q=2π\int{^R_0}v_zrdr$
After substituting equation 9 in for $v_z$ and integrating equation 11 the following equation will result.
(Eq 12) $Q=-\frac{πR^4}{8μ}\left(\frac{∂p}{∂z}\right)$
Next, the pressure differential can be related to the pressure drop across a certain length of interest of the tube.
(Eq 13) $\frac{Δp}{l}=-\frac{∂p}{∂z}$
As a result, equation 12 can be modified to the following equation.
(Eq 14) $Q=\frac{πR^4Δp}{8μl}$
From this equation it can seen that the volume flow rate is inversely proportional to the viscosity and proportional to the tube radius raised to the fourth power. In turn, if you were to double the tube’s radius you would be able to increase the flow rate by 16 times for the pressure drop per unit length. This is known as Poiseuille’s law.
In addition, the mean velocity can be found using the volume flow rate, where $v=Q/πR^2$. As a result, the mean velocity can be found using the following equation.
(Eq 15) $v=\frac{R^2Δp}{8μl}$
Finally, to find the maximum velocity, which will occur in the center of the tube, the following equation will be used.
(Eq 16) $v_{max}=-\frac{R^2}{4μ}\left(\frac{∂p}{∂z}\right)=\frac{R^2Δp}{4μl}=2v$