A Rankine oval is is created by superimposing a uniform flow with a source and a sink. As the distance between the source and sink decreases to zero, the Rankine oval will become more blunt. Eventually, the shape of the Rankine oval will become a circle. Hence, when this occurs we will be able to analyze the flow around a circular cylinder. However, in order to satisfy Laplace’s equations the flow must be assumed to be irrotational. The combination of a uniform flow with a doublet will give us the following stream function.
(Eq 1) $ψ=Ur~sin~θ-\frac{K~sin~θ}{r}$
In turn, the resulting velocity potential will become the following.
(Eq 2) $Φ=Ur~cos~θ+\frac{K~cos~θ}{r}$
Next, the stream function for flow around a circular cylinder will need to be determined. To do this the following will apply; $ψ=constant$ for $r=a$ where $a$ is the radius of the cylinder. As a result, equation 1 is rewritten to the following.
(Eq 3) $ψ=\left(U-\frac{K}{r^2}\right)r~sin~θ$
Hence, when $ψ=0$ for $r=a$ the following will result.
(Eq 4) $U-\frac{K}{a^2}=0$
In turn, this indicates that $K$, which represents the doublets strength, will be equal to $Ua^2$. Due to this fact, the stream function for flow around a cylinder becomes the following equation.
(Eq 5) $ψ=Ur\left(1-\frac{a^2}{r^2}\right)~sin~θ$
In addition, the corresponding velocity potential can be seen below.
(Eq 6) $Φ=Ur\left(1+\frac{a^2}{r^2}\right)~cos~θ$
From the stream function and velocity potential, the velocity components of the flow can be determined.
(Eq 7) $v_r=\frac{∂Φ}{∂r}=\frac{1}{r}\frac{∂ψ}{∂θ}=U\left(1-\frac{a^2}{r^2}\right)~cos~θ$
and
(Eq 8) $v_θ=\frac{1}{r}\frac{∂Φ}{∂θ}=-\frac{∂ψ}{∂r}=-U\left(1+\frac{a^2}{r^2}\right)~sin~θ$
Finally, the maximum velocity will occur on the surface of the cylinder at $r=a$ causing $v_r=0$ and $v_{θs}=-2U~sin~θ$. In turn, this will occur in two places, the top and bottom of the cylinder $(θ=±π/2)$.
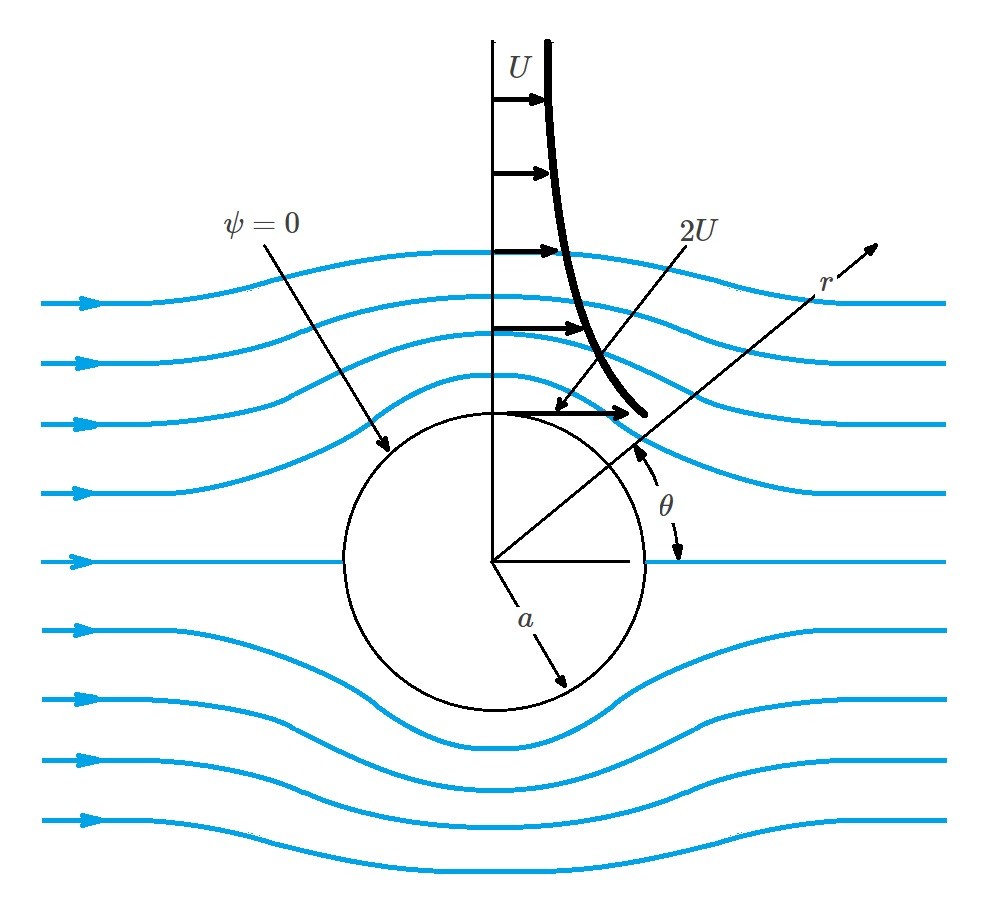
Surface Pressure
Now that the velocity is known, the pressure distribution across the cylinder surface can be determined. In order to do this Bernoulli equation will be used. However, to use Bernoulli equation you will need to pick a point far enough away from the cylinder where the pressure is $p_o$ and the fluid velocity is $U$. Elevation changes will be neglected.
(Eq 9) $p_o+\frac{1}{2}ρU^2=p_s+\frac{1}{2}v^2_{θs}$
In the above equation $p_s$ represents the surface pressure on the cylinder. Due to the fact that $v_{θs}=-2U~sin~θ$, the surface pressure can be expressed as the following.
(Eq 10) $p_s=p_o+\frac{1}{2}ρU^2(1-4~sin^2~θ)$
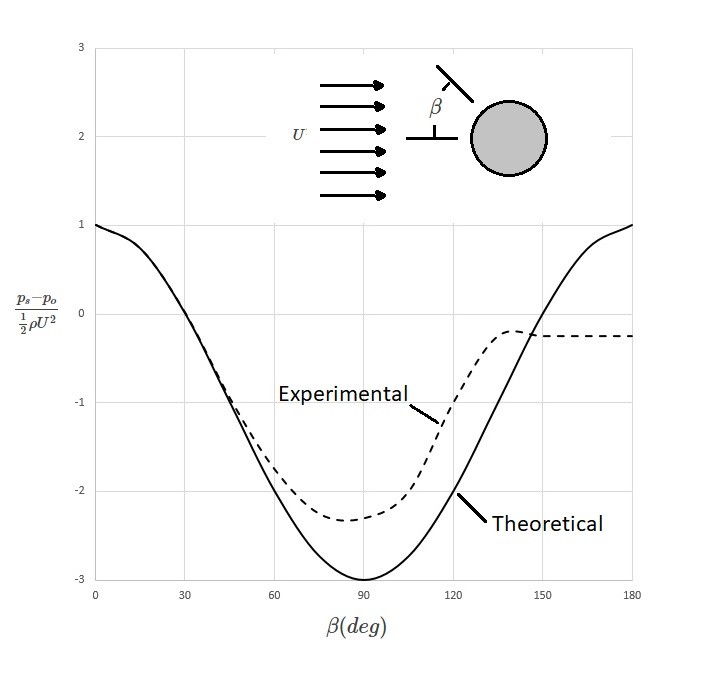
The above image is a comparison of experimental data to theoretical data expressed in dimensionless form. From this image it can be concluded that there is only approximate agreement on the upstream portion of the cylinder. On the other hand, the down stream side varies greatly. This is due to the viscous boundary layer that develops on the cylinder as the flow separates from the surface.
Surface Forces
In addition to the surface pressure for flow around a circular cylinder, the surface forces can also be determined. By integrating the pressure over the cylinders surface, the resultant force per unit length can be determined.
(Eq 11) $F_x=-\int{^{2π}_0}p_s~cos~θ~a~dθ$
and
(Eq 12) $F_y=-\int{^{2π}_0}p_s~sin~θ~a~dθ$
In the above equations $F_x$ represents drag, which is the force parallel to the uniform flow. In addition, $F_y$ represents lift, which the force that is perpendicular to the uniform flow. However, when equation 10 is substituted for $p_s$ both $F_x$ and $F_y$ will equal zero. Hence, when drag and lift is predicted by the potential theory for a uniform flow around a fixed cylinder, the resulting forces will be zero. This is due to the pressure distribution around the cylinder being symmetrical. However, in reality there will a drag force when the cylinder is placed in a moving fluid. This is due to Alembert’s paradox, where a french mathematician Jean le Rond d’Alembert stated that the drag on bodies immersed in an inviscid fluid will be zero. However, he did not consider the effects of a viscous fluid, hence the paradox.
Free Vortex
In addition to the above, a free vortex can be added to the uniform flow doublet combination. In turn, this will result the following stream function and velocity potential for flow around a circular cylinder.
(Eq 13) $ψ=Ur\left(1-\frac{a^2}{r^2}\right)~sin~θ-\frac{Γ}{2π}~ln~r$
and
(Eq 14) $Φ=Ur\left(1+\frac{a^2}{r^2}\right)~cos~θ+\frac{Γ}{2π}θ$
In the above equations $Γ$ represents circulation. In addition, for a circle $r=a$ will still be a streamline. The reason this is because the added free vortex is circular. As a result, the tangential velocity, $v_θ$ on the surface of the cylinder can found using the following equation.
(Eq 15) $v_{θs}=-\frac{∂ψ}{∂r}|_{r=a}=-2U~sin~θ+\frac{Γ}{2πa}$
To create this type of flow field you would need to place a rotating cylinder into a uniform flow field. In turn, the rotating cylinder will create a free vortex. A variety of different patterns can develop depending on the strength of the free vortex. However, the type of pattern that will develop is dependent on the location of the stagnation point on the surface of the cylinder.
(Eq 16) $sin~θ_{stag}=\frac{Γ}{4πUa}$
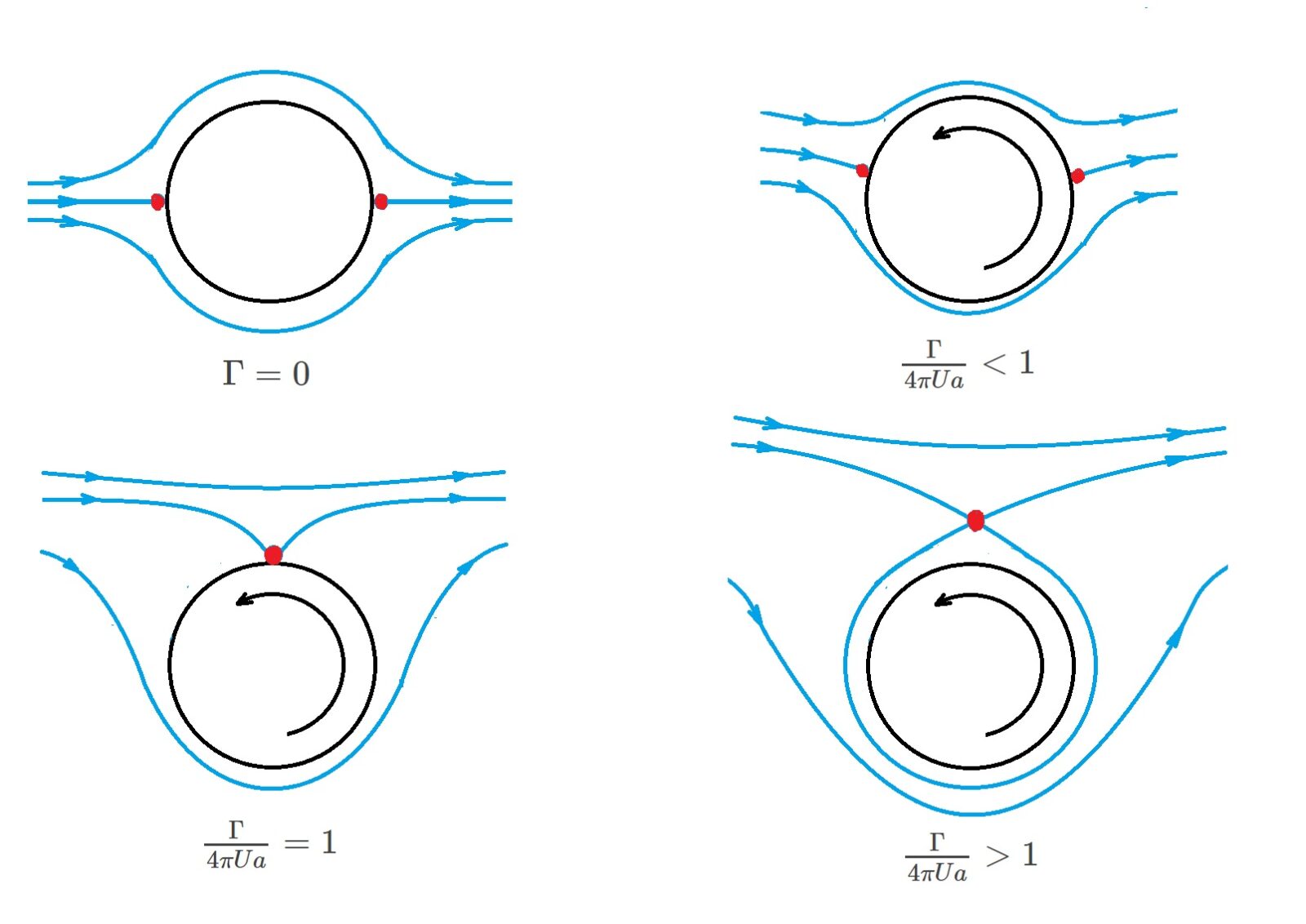
From the image it can be seen that when there is no circulation, or $Γ=0$, than the stagnation points will occur at $θ=0~or~π$. On the other hand, if $-1≤Γ/4πUa≤$ than the stagnation points will occur on some other location on the surface of the cylinder. Finally, if $Γ/4πUa$ is greater than 1 the stagnation point will occur off of the surface of the cylinder.
Pressure and Force Free Vortex
Finally, as before, Bernoulli equation is used to determine the surface pressure on the cylinder.
(Eq 17) $p_o+\frac{1}{2}ρU^2=p_s+\frac{1}{2}ρ\left(-2U~sin~θ+\frac{Γ}{2πa}\right)^2$
or
(Eq 18) $p_s=p_o+\frac{1}{2}ρU^2\left(1-4~sin^2~θ+\frac{2Γ~sin~θ}{πaU}-\frac{Γ^2}{4π^2a^2U^2}\right)$
Next the forces per unit length is obtained by integrating the differential pressure around the circumference of the cylinder. In turn this will allow us to determine the drag force $F_x$ and the lift $F_y$.
(Eq 19) $F_x=0$
and
$F_y=-ρUΓ$