As a rigid body moves through space one type of motion that it could subjected to is translation. To further break this down a rigid body could have have either rectilinear or curvilinear translation. Rectangular translation means that the rigid body is moving on a straight line. While curvilinear translation means that the rigid body is moving around a curved path. Translation occurs when a line segment between two particles within the rigid body remain parallel to to each other while the rigid body move along its path.
Position
Like a particle, a rigid body that is moving through space will have a certain coordinate position. An observer has to determine the rigid bodies position in space. Because of this the rigid bodies position is subjective.
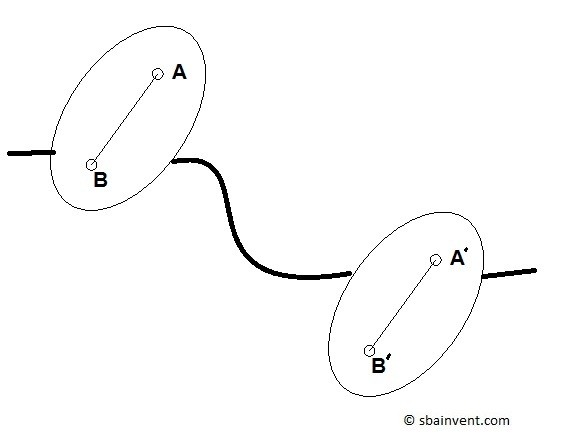
Remember that a rigid body is made out of many particle. Each particle will have its own unique coordinate position. The position of each particle can be related to each other by using relative position of a particle as seen in the equation below.
(Eq 1) $r_B=r_A+r_{B/A}$
Velocity
As a rigid body moves through space its position will change within a certain time period. The change in position in respect to a change in time will result in a velocity. To calculate the velocity you would take the derivative of the position in respect to time as seen in the equation below.
(Eq 2) $v=\frac{ds}{dt}$
The above statement is true for both a rigid body and a particle. However, we also need to consider how the particles within the rigid body relate to each other. If a rigid body is only subject to translation than all of the particle within it will see the same velocity.
(Eq 3) $v_B = v_A$
Acceleration
When a rigid body is moving through space there is a possibility of a change in velocity, which would result in an acceleration. To find the acceleration due to a change in velocity you would take the derivative of the rigid body’s velocity in respect to time, or the double derivative of it position in respect to time.
(Eq 4) $ a=\frac{dv}{dt}=\frac{d^2s}{dt^2}$
As with velocity, the above statement is true for both rigid bodies and particles. We will need to determine how particles in the rigid body relate to each other. If the rigid body is only subject to translation, like velocity, the acceleration of all the particles will be the same.
(Eq 5) $a_B=a_A$