The linear momentum of a particle is the product of the particles mass and its velocity. Due to this momentum is a vector quantity. As a result the units would be $\frac{kg-m}{s}$ for SI units are $\frac{slug-ft}{s}$ for imperial units.
Momentum is dependent on a frame of reference, meaning that an observer observes the particles velocity from a certain frame of reference. Hence the frame of reference could be stationary, or it could be translating. Momentum, however, is a conserved quantity in any inertial frame. As a result the linear momentum will not change when you are observing a closed system with not external forces applied.
(Eq 1) $p=mv$
For example if an observer was watching an object from outside an elevator, where the elevator is moving at a constant velocity, would say that the object has a linear moment that is related to the speed of the elevator. On the other hand, if there is an observer inside that same elevator, they would say that the same object has zero momentum since they can’t observe the velocity of the elevator, even though we know that the object has a linear momentum that is related to the speed of the elevator. However, if the speed of the elevator changes, such as when it stops, the observer inside the elevator will feel a change in momentum, due to the elevator decelerating and then would be able to observe a linear moment due to external forces acting on the elevator.
The above example can be explained by Newton’s second law which states that a “body’s change in momentum is equal to the net force acting on it.” Due to this fact, the force acting on a particle can be related to its velocity using the following equation, where the force integrated over a set period of time is an impulse and the product of the mass and velocity is the particles linear momentum.
(Eq 2) $mv_1+∑∫_{t_1}^{t_2}Fdt=mv_2$
$m$ = mass
$F$ = force
$v_1$ = initial velocity
$v_2$ = final velocity
Finally, the above shows that momentum is the ability a particle has to resist a change in direction or velocity. On the other hand an impulse is a force integrated over time that will cause a change in momentum.
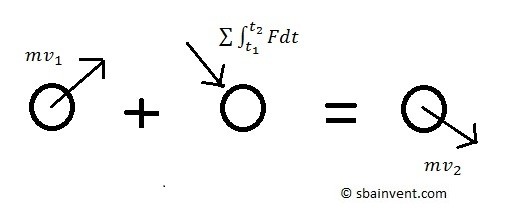
Example
A car is traveling down a highway at 60 mph. The car weighs 3000 lbs and the kinetic coefficient friction of the tires and pavement is 0.3. If the car goes into a skid when the brakes are applied, how fast will the car stop? How far will the car have traveled before it comes to a complete stop?
Solution
60mph = 88$\frac{ft}{s}$
Step 1: Determine the force the tires exert due to kinetic friction.
$F=(3000)(0.3)=900lb$
Step 2: Using equation 2 determine the time it takes for the car to stop.
$900(t)=\frac{3000}{32.2}(88)$
$t=\frac{8199}{900}=9.1~s$
Step 3: Determine the rate of deceleration.
$a(t)+v_o=v$
where $v_o = 88\frac{ft}{s}$ and $v = 0\frac{ft}{s}$
$a=\frac{-88}{9.1}=-9.67\frac{ft}{s^2}$
Step 4: Determine the distance traveled.
$ s = s_o + v_ot + \frac{1}{2}at^2$
where $s_o=0$
$s=88(9.1)-\frac{1}{2}(9.67)(9.1^2)= 400.4~ft$