I have mainly talked about absolute motion (motion observed by a stationary observer) in the articles preceding this article. There can however be many cases where the motion of a particle could be so complex that it would be difficult to analyze by observing it from one stationary point. Hence to simplify complex problems you can observe the motion from multiple frames of reference. An example of this could be analyzing the tip of a ships propeller. For instance, a fixed observer would see the ship itself moving, while another observer would analyze the propellers rotation. As a result to find the complete motion of the propeller you would superimpose the two observations vectorially.
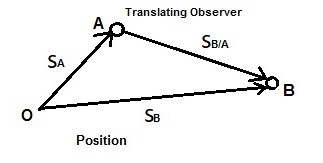
Position
Let’s consider two particles that are moving in a straight line in different directions. First, there will be a stationary observer at point O observing both particle A and particle B. Next, a translating observer will view the motion of particle B from particle A. Paths $s_A$ and $s_B$ are absolute paths. While path $s_{B/A}$ is a relative position. Finally, the three paths can be related to each other using vector addition.
(Eq 1) $s_B=s_A+s_{B/A}$
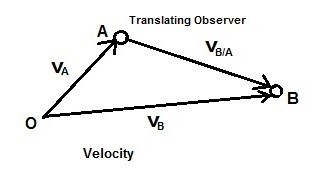
Velocity
If you were to take the derivative of equation 1 you would be able to find the velocity of particle A and particle B. This would result in the equation below.
(Eq 2) $v_B=\frac{ds_B}{dt}$, $v_A=\frac{ds_A}{dt}$, $v_{B/A}=\frac{ds_{B/A}}{dt}$
For the above equation, velocities $v_B$ and $v_A$ are absolute velocities. The third velocity $v_{B/A}$ will be a relative velocity. In turn, the velocities can be related to each other through vector addition as seen in the equation below.
(Eq 3) $v_B=v_A+v_{B/A}$
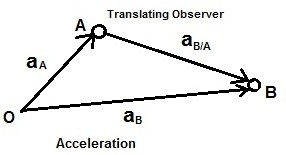
Acceleration
Finally, if you were take the derivative of equation 1 or the double derivative of equation 3 you will be able to find the acceleration of particle A and particle B.
(Eq 4) $a_B=\frac{dv_B}{dt}$, $a_A=\frac{dv_A}{dt}$, $a_{B/A}=\frac{dv_{B/A}}{dt}$
In the above equation $a_B$ and $a_A$ represent the absolute acceleration of the two particles, while $a_{B/A} represents the relative acceleration between particle A and particle B. The absolute accelerations and relative acceleration can be related to each other through vector addition as seen in the equation below.
(Eq 5) $a_B=a_A+a_{B/A}$
Example
What is the magnitude and direction of the relative velocity of particle A in respect to particle B?
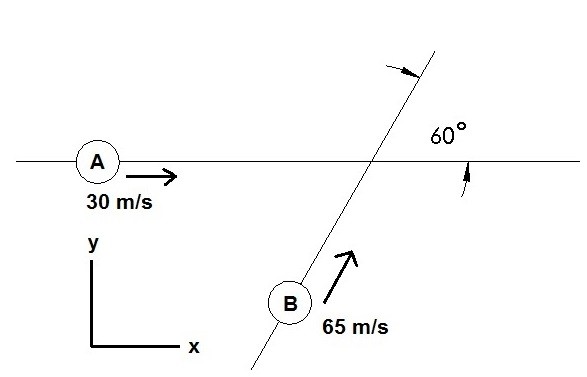
Solution
Step one, use equation 3 and write the velocity components out in x and y coordinates.
$30i=(65cos(60)i+65sin(60)j)+V_{A/B}$
Solve for $V_{A/B}$
$V_{A/B}=(-2.5i-56.3j)\frac{m}{s}$
Find the magnitude of the velocity and angle.
$V_{A/B}=\sqrt{2.5^2+56.3^2}=56.4\frac{m}{s}$
$tan(θ)=\frac{-56.3}{-2.5}$, $θ=87.5^o$![]()