General plane motion occurs when a rigid body experiences translation and rotation simultaneously. You can analyze a problem like this by either using absolute motion analysis or relative motion analysis.
Absolute Motion Analysis
When both translation and rotation are occurring, determining the motion of a problem can become complex. For instance, one type of analysis that you can use is absolute motion analysis. Absolute motion can only be used when one fixed reference can be used to solve the problem.
The following steps would be used to solve a general motion problem using absolute motion analysis. First, you will need to determine a point of interest on the rigid body. After that you need to locate the position of the point based of a fixed origin using rectilinear position coordinates. As a result these two steps will allow you to analyze the translation part of the problem.
There is also a rotational part of the problem which will need to be related to translation. First, you will need to measure fixed reference lines that relate the axis of rotation and the point of interest to the angular position θ. Than, you will need derive an equation (s=f(θ)) to determine the position of the point of interest. You can derive the position equation by using both geometry and trigonometry. Finally, you can find velocity and acceleration by taking the derivatives of the position equation in relation to time.
Example
Below is an example of a simple cam. A circular disk is rotating about point O. A rod makes contact with the disk at point P where the fixed line connecting point P to point O will remain parallel to the center point of the disk at point A. Determine the position equation for point p in respect to x.
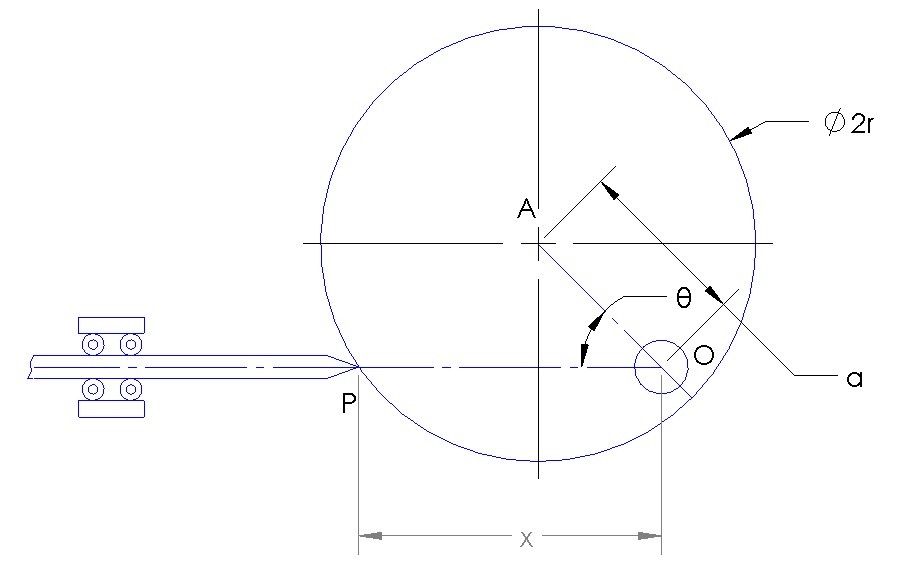
Solution
Step 1: Determine the position equation.
There are two methods that can be used. While using these methods you need to recognize that the offset (a) of the pivot point O does not change and the radius (r) of the disk doesn’t change. x and θ do change as the disk rotates.
First, you can use the law of cosines to relate x to θ.
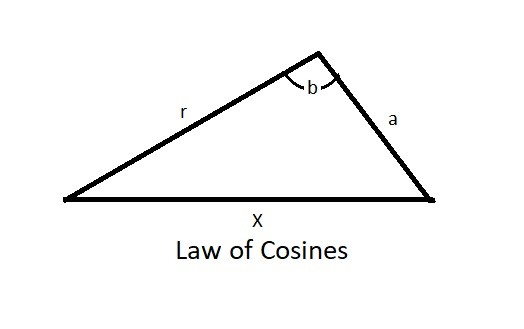
$x=\sqrt{a^2+r^2-2ar~cos(b)}$
where $b= cos^{-1}\left(\frac{a~sinθ}{r}\right)+\left(\frac{π}{2}-θ\right)$
You can also find the position equation by using simple trigonometry and the Pythagorean theorem.
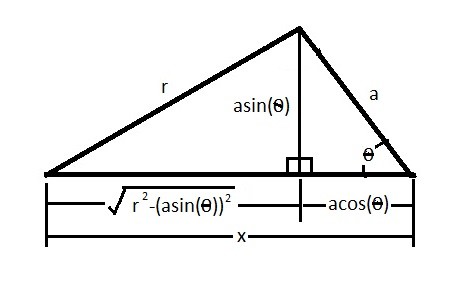
$x=\sqrt{r^2-(asinθ)^2}+acosθ$
From the above equation the velocity and acceleration can be determine by taking the derivative in respect to time. For velocity you would take the derivative of θ in respect to time. While for acceleration you would take the derivative of θ and of ϖ of the velocity equation in respect to time to represent tangential and normal acceleration. It is possible to find the velocity and acceleration equations for the example above. However, for simplicity, I show how to find the velocity and acceleration equations for a simple position equation below.
Example
Calculate the velocity and acceleration equation for the following equation, where θ represents angular position and ϖ represents angular velocity.
$x = 2r~cos(ϖ)$
Solution
The chain rule of calculus will have to be used to find the derivatives of the above equation.
- Velocity Equation
$\frac{dx}{dt}=-2r(sin~θ)\frac{dθ}{dt}$
or
$v=-2rϖsinθ$
- Acceleration Equation
$\frac{dv}{dt}=-dr\left(\frac{dϖ}{dt}\right)sinθ-2rϖ(cosθ)\frac{dθ}{dt}$
or
$a=-2r(αsinθ+ϖ^2cosθ)$
The above equations would apply to the disk in the first example if the pivot point were at the edge of the disk but still inline with point P.