As a body moves through space it will have a momentum. Which is based off of its mass as well as its velocity. As a result the greater its mass or its velocity the greater its momentum. On the other hand an impulse is a force acting on a body within a certain time period. An impulse has the capability of changing a bodies momentum.
Momentum of a Rigid Body
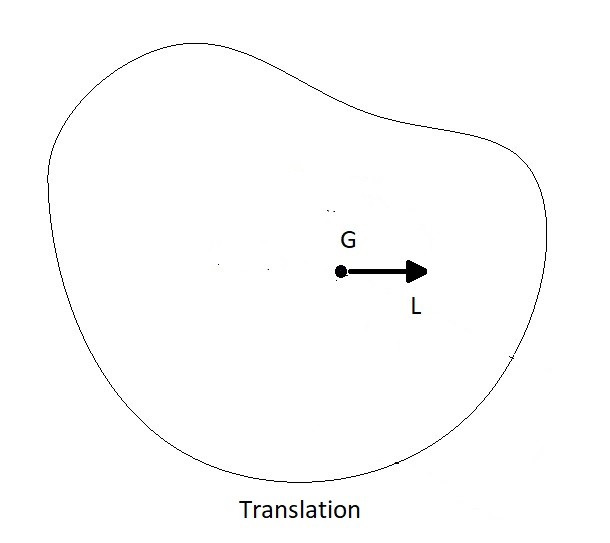
Translation
When a rigid body move through space it can have translational motion or rotational motion. If you are analyzing the momentum of its translational motion you will need to know the magnitude of its velocity from its x, y, and z components. You will all need to know what the bodies mass is. Once you know these values you find linear momentum in a specific direction by using the equation below.
(Eq 1) $L=mv_G$
$m$ = mass
$v_G$ = velocity
$L$ = Linear Momentum
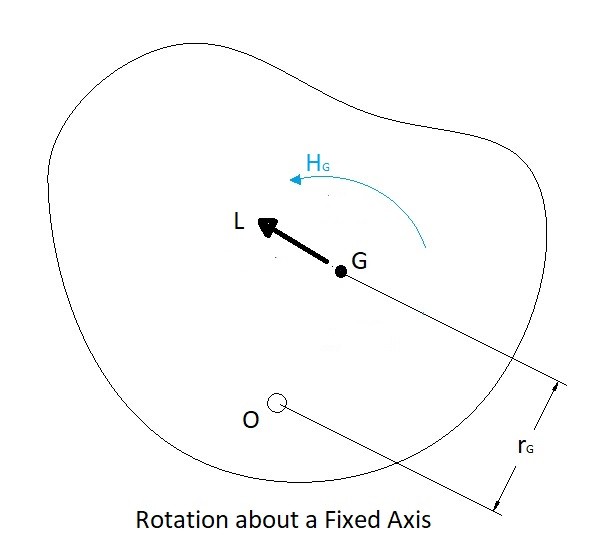
Rotation around a Fixed Axis
Next, as mentioned above, a rigid body will also have the capability of rotational velocity, which differs from a particle. When a rigid body rotates, you will need to determine the bodies mass moment of inertia around the axis of rotation in addition to its angular velocity. Once you know these values you can determine its angular momentum around the center of mass by using the equation below.
(Eq 2) $H_G=I_Gϖ$
$I_G$ = Mass Moment of Inertia
$ϖ$ = Angular Velocity
$H_G$ = Angular Momentum
There can be times when the body is rotating around a point that is offset from the center of mass of the body. If this is the case equation 2 would have to be modified to the following equation.
(Eq 3) $H_O=I_Gϖ+r_G(mv_G)=I_Oϖ$
This equation will allow you to find the angular momentum around point O for the image below.
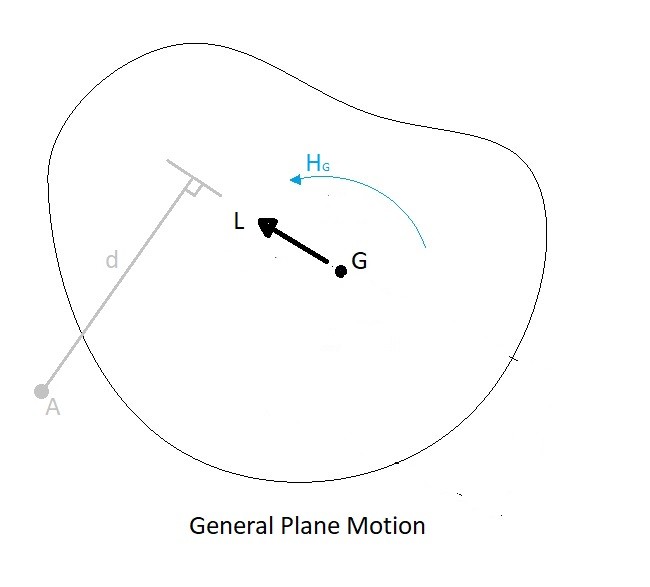
General Plane Motion
Finally, general motion has a combination of translational motion and rotation. In turn an objection that has general motion will have both linear and angular momentum. Regardless of the point of interest the linear momentum will always be calculated using equation 1. However, if the point of interest isn’t on the center of mass, than the angular momentum equation would have be modified.
(Eq 4) $H_A=I_Gϖ+d(mv_G)=I_Aϖ$
The above equation will allow you to find the angular momentum at the arbitrary point A on the image below. You should notice that equation 3 and 4 are the exact same equation.
Impulse of a Rigid Body
So far I have only talked about momentum regarding a constant velocity. However, as we know, velocity can change over time if there is a force or a moment acting on the body.
Linear Impulse and Momentum
As mentioned previously, a rigid body can have a mixture of translational motion and rotational motion. First, lets discuss translation. To change the velocity, and in turn change the momentum of the body, a force will need to applied to the rigid body to create an acceleration or deceleration. If you integrate the force in respect to time you will find the linear impulse acting on the body. This will be equal to the change in linear momentum.
(Eq 5) $m(v_G)_1+\sum{}∫^{t_2}_{t_1}Fdt=m(v_G)_2$
$F$ = Force
Angular Impulse and Momentum
Finally, an object that is rotating will have certain angular momentum. If a moment was placed on the body its angular velocity will change in respect to time do to the moment causing an angular acceleration or deceleration. In turn if you were to integrate the moment in respect to time you will find the angular impulse that the moment places on the rigid body. The angular impulse will be equal to the change in the angular momentum of the rigid body.
(Eq 6) $I_Gϖ_1+\sum{}∫^{t_2}_{t_1}M_Gdt=I_Gϖ_2$
$M$ = Moment
Example
A pulley of uniform mass initially at rest has a constant mass of 5kg pulling down on it. Determine angular velocity of the pulley after 5 second, as well as the forces on the axle supporting the pulley. The pulleys mass is 12 kg and a diameter of 76 mm.
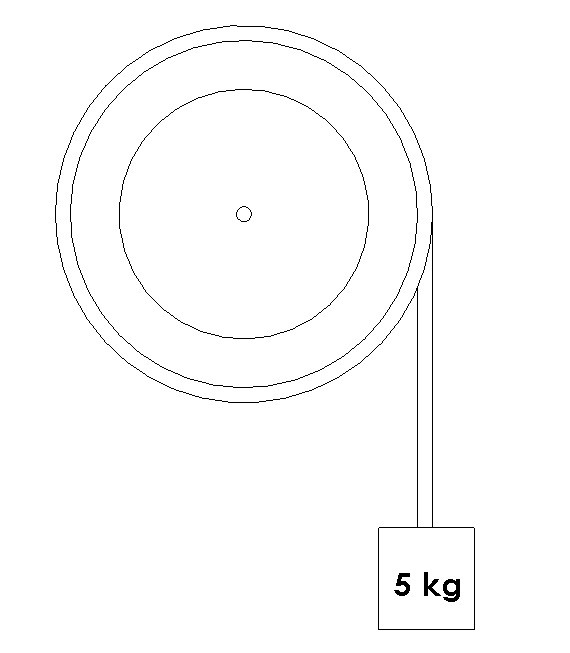
Solution
Step 1: Draw a free body diagram to account for all of the forces acting on the pulley.
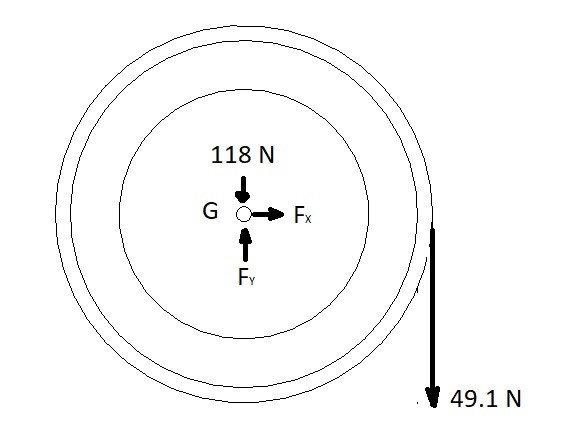
Step 2: From the FBD generate the impulse and momentum equations from equations 5 and 6.
x-direction linear momentum
$m(v_{G_x})_1+\sum{}∫^{t_2}_{t_1}F_xdt=m(v_{G_x})_2$
$0 + F_x(5~s) = 0$
y-direction linear momentum
$m(v_{G_y})_1+\sum{}∫^{t_2}_{t_1}F_ydt=m(v_{G_y})_2$
$0 + F_y(5~s) – (118~N)(5~s)-(49.1~N)(5~N) = 0$
angular momentum
$I_Gϖ_1+\sum{}∫^{t_2}_{t_1}M_Gdt=I_Gϖ_2$
$I_G = \frac{1}{2}mr^2$$=\frac{1}{2}(12~kg)(.038~m)^2=.0087~kg·m^2$
$0+(49.1~N)(.038~m)(5~s)=.0087ϖ_2$
Step 3: Solve for the variables.
$F_x = 0$
$F_y = 167.1~N$
$ϖ_2 = 1072\frac{rad}{s}~clockwise$