A rigid body can have two different type of motion. They are translation or rotation about fixed axis. In a previous article I discussed translation. Instead in this article I will focus on rotation about a fixed axis.
If a rigid body is rotating about a fixed axis, the particles will follow a circular path. The further a particle is from the axis of rotation, the greater the angular velocity and acceleration will be. On the other hand, any particle that are located on the axis of rotation will be stationary.
Angular Displacement
The angular displacement, expressed in radians, is the distance that a particle moves as the rigid body rotates. However, since angular displacement is in radians you will need to convert degrees to radians. You can convert degrees to radians by using the equation below.
(Eq 1) $radians = degrees\left(\frac{π}{180^o}\right)=θ$
$1~rev=360^o=2π$
All particle, except those located on the fixed axis, will have the same angular displacement. On the other hand, particles located on the fixed axis will have no displacement.
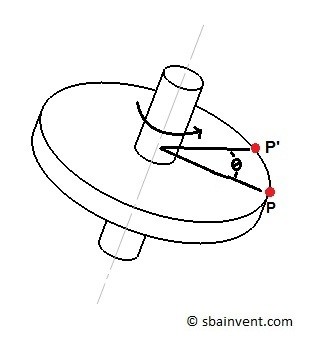
The actual distance that the particles travel will be greater the further the particle is from the axis of rotation. To find how far a particle has traveled, use the equation below.
(Eq 2) $s_t=θr$
r = distance from axis of rotation
Angular Velocity
As a rigid body is rotating around a fixed axis it will be rotating at a certain speed. To find angular velocity you would take the derivative of angular displacement in respect to time.
(Eq 3) $ϖ=\frac{dθ}{dt},~units~\left(\frac{rad}{s}\right)$
All particles will have the same angular velocity, with the exception of particle on the fixed axis. As a result, particles on the fixed axis will have no angular velocity.
Tangential velocity will increase the further the particle is from the fixed axis. Therefore to find the tangential velocity at a specific point you would use the following equation.
(Eq 4) $v_t=ϖr$
Finally, people usually express angular velocity in rotations per minute (rpm). As a result you can convert radians per second to rotations per minute by using the equation below.
(Eq 5) $rpm=\frac{60ϖ}{2π}$
Angular Acceleration
An angular acceleration is the result of the angular velocity changing. Therefore to find angular acceleration you would take the derivative of angular velocity in respect to time. In addition, you could also take the double derivative of angular displacement in respect to time.
(Eq 6) $α=\frac{dϖ}{dt}=\frac{d^2θ}{dt^2},~units~\left(\frac{rad}{s^2}\right)$
All particle will have the angular acceleration, accept those located on the fixed axis. On the other hand particles on the fixed axis will have no angular acceleration. Furthermore, normal and tangential acceleration will increase the further the particle is from the fixed axis.
(Eq 8) $a_t=αr$
(Eq 9) $a_n=ϖ^2r$
You should notice from the above equations that normal acceleration is independent of angular acceleration. As a result normal acceleration will occur even when the angular velocity is constant. Hence to find the total acceleration at a point, use the equation below.
(Eq 10) $a=\sqrt{a_n^2+a_t^2}$