Applying a force to a rigid body will transfer a certain amount of energy known as work into the body. You can determine the amount work caused by a force by finding the total displacement caused by the force.
The Work of a Force
(Eq 1) $U_f=F·r=\int_s{}Fcosθds$
Equation 1 is the general equation that is use to determine work caused by a force. For the above equation the rigid body will be following a path represented by s, while θ represents the angle of the force vector and the differential displacement. Generally, unless already known, the integration will need to take in account for variations in the force’s direction and magnitude.
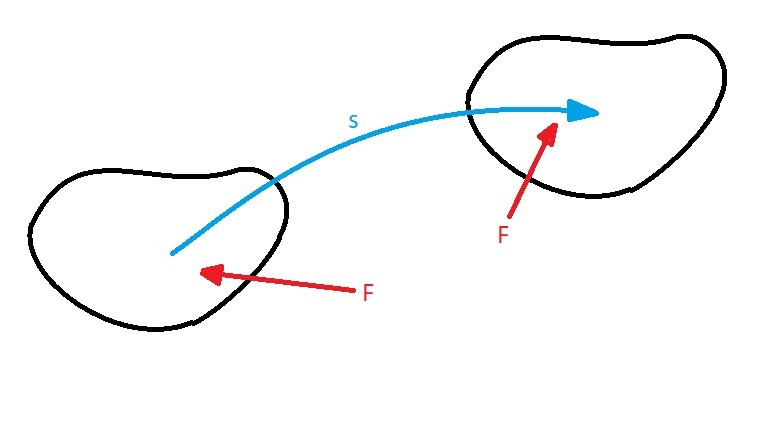
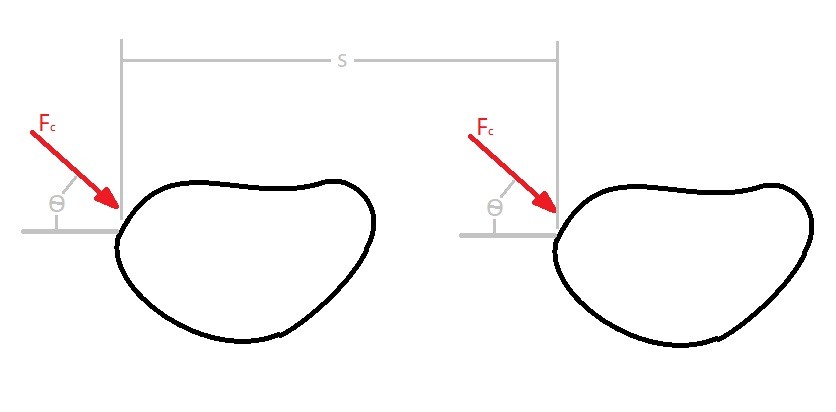
In certain cases the magnitude of the force will remain the same as well as the direction of the force vector. This will cause the following modification to equation 1.
(Eq 2) $U_{F_c} = (F_ccosθ)s$
The Work of a Couple Moment
Both particles and rigid body’s follow the same principles for finding the work caused by a force. However, unlike a particle, a rigid body can rotate as well as have translation. While a particle will only have translation.
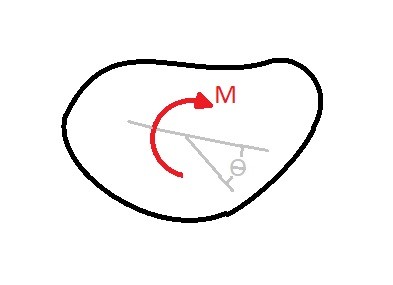
Just like a force will generate a certain amount of work along a translational path. A moment will generate a certain amount of rotational work. To find the rotational work you will need to know the coupling moment and amount angular displacement caused by the coupling moment.
(Eq 3) $U_M=\int_{θ_1}^{θ_2}{}Mdθ$
Equation 3 is the general equation that is use to determine work caused by a coupling moment. There can be cases where the coupling moment will be constant. This will cause the following modification to equation 3.
(Eq 4) $U_M=M(θ_2-θ_1)$
For both work caused by a force, and work caused by a moment, the energy will create either a potential energy situation or a kinetic energy situation. When work is storing energy, such as in a spring, you have potential energy situation. On the other hand if the work is causing motion than you have a kinetic energy situation.