Applying a force to a particle would result in the particle moving a certain distance.. In turn this means that the force is inputting a certain amount of energy into that particle. As a result the force is doing work which is a type of energy. If you are using the standard international system, energy units will be represented by Joules (J).
$1J = 1N•m$
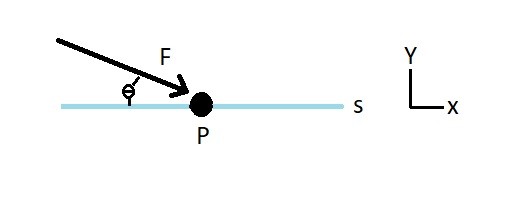
Let’s take a look at the image above. For this case we will have particle P restrained so that it will only following path s. This path happens to move along the axis of the coordinate system. In addition there is a force acting on the particle at an offset angle. As a result we will need to determine what portion of the force is acting in the x-direction. Once we know this we can determine the amount of work force F has performed.
Eq 1 $du=Fdscosθ$ or $\int_{s_1}^{s_2}Fcosθds$
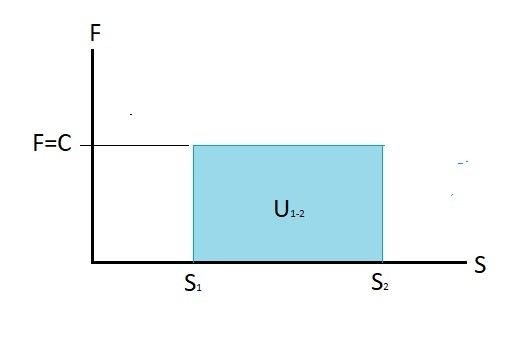
You can calculate energy by taking the integral of the force curve. As a result work is actually the area under the force curve.
Power
Once you know what the energy is you can than determine how much power was needed to move the particle. Power is an integral of energy in respect to time. Refer to equation 2.
(Eq 2) $P=F·V=\frac{dU}{dt}$
F = force
V = Velocity
P = Power
dU = Change in Energy
dt = Change in Time
Equation 2 represents the power input for a particle that has a linear projection. In addition to linear power there is also rotational power. To find this value you would need to use equation 3.
(Eq 3) $P=Tϖ$
T = Torque
ϖ = angular velocity
There are a variety of units that can be used to express power. To familiarize yourself with some of them refer to equation 4.
(Eq 4) $1W=1\frac{J}{S}=1\frac{N·m}{s},~or~1hp = 550\frac{ft·lb}{s}$
Finally, there will always be some energy lost to drag or friction. To determine the efficiency of the system you will need to determine the ration of the input and out put power.
(Eq 5)$ε=\frac{energy~output}{energy~input}$
Problem
A car is accelerating onto the highway. It has the capability to go from 0-60 mph in 7 seconds. The car’s weighs 3500lb. If the car is accelerating as fast as it can how much energy will be required for the car to reach 60mph? How much power will need to transmitted to the wheels of the car? The on-ramp is on a flat surface.
Solution
Step 1: Determine the cars acceleration.
$60mph = 88\frac{ft}{s}$
$a=\frac{88}{7}=12.6\frac{ft}{s^2}$
Step 2: Determine the force transmitted to the wheels of the car.
$F=(\frac{3500}{32.2})(12.6)=1370 lb$
Step 3: Determine the distance the car traveled before reaching full acceleration.
$s=12.6(7^2)=617~ft$
Step 4: Determine the energy required for the car to accelerate to 60mph in 4 seconds.
$U_{1-2}=1370(617)=845290~ft·lb$
Step 5: Determine the power that will need to be transmitted to the wheels of the car.
$P=\frac{845290}{7}=120755\frac{ft·lb}{s}=220~hp$