As a particle moves through space it will have a certain position. As time progresses the moving particle’s position will change. Its position will be based off of the Cartesian coordinate system. This means it will have certain position in the x-direction, a certain position in the y-direction, and a certain position in the z-direction. Its initial position will be subjective to an observer. That observer defines its initial position, and if their is a second observer it is possible they may define a completely different initial position. Both observers though should observe the same change in position in relation to time.
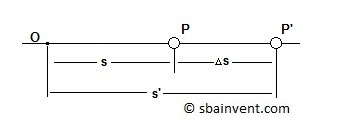
In order to find displacement of a particle you would use equation 1. Note, the figure below shows the change in position is in a straight line. However you should realize that the particle could actually be zigzagging through space. Even though this could be the case the position for a given time would be the same since only two points are being observed.
(Eq 1) $Δs = s’-s$
$s$ = Original Position from origin
$s’$= New position from origin
$Δs$ = Change in position
Example
If a particle initial position is 4 miles from observer A than after a certain amount of time its new position is 10 miles from observer A, what was its change in position? What would its initial position be for observer B in respect to observe A if observer B is 5 miles closer to the object at its final position than observer A. Assume that observer A, observer B, and the object are all in line with each other and that observer A and observer B are stationary.
Answer
Using equation 1 the objects position of origin is 4 miles from observer A and its new position is 10 miles from observer A. You can modify equation 1 to the following.
$10-4=6~miles$
Now observer B is 5 miles closer to the object than observer A. When the object reaches it final position this means that according to observer B it final position would be the following.
$10-5= 5~miles$
While the objects initial position for observer B would be the following.
$5-6=-1~miles$ or 1 mile behind observer B.
Notice that even though the object’s change in position is 6 miles, observer A and observer B see two different things. Observer A sees the object move away from them by 6 miles, while Observer B initially sees the object 1 miles behind them and than the object will pass them and reach its final position 5 miles in front of them. This is why I said position is subjective to the observer.
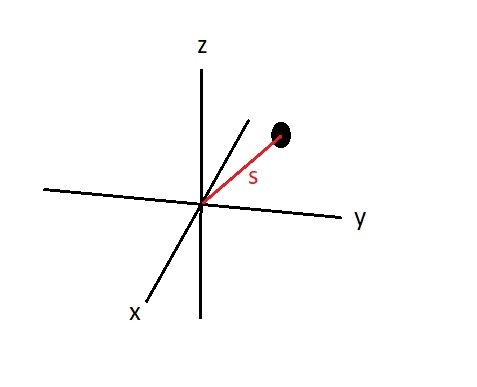
Now remember we live in a 3 dimensional world. Since we live in 3 dimensional world you will most likely have to define a particles position in the x, y, and z directions. Due to this fact we can use equation 1 to say that the particle has move in the x-axis a certain amount, the y-axis a certain amount, and the z-axis a certain amount. However, this doesn’t give us clear picture on how far the particle moved from position A to position B. To clarify this we can use equation 2 to determine the position vector, which will define the distance between point A and point B by finding the magnitude of the x, y, z coordinates.
(Eq 2) $r=\sqrt{xi^2+yj^2+zk^2}$
$xi$ = Position in the x-direction
$yj$ = Position in the y-direction
$zk$ = Position in the z-direction
Example
A particle is located at a point in space at the following coordinates 5i, 6j, 2k. After a certain period of time passes the new position of the particle is 3i, 2j, 7k. Determine the magnitude of the change in position.
Answer
Use equation 1 to determine the change in the x, y, z axis.
x-direction
$3i-5i=-2i$
y-direction
$2j-6j=-4j$
z-direction
$7k-2k=5k$
Use equation 2 to determine the magnitude of the change in position.
Magnitude of position change
$\sqrt{(-2i)^2+(-4j)^2+(5k)^2}=6.71$