A projectile is an object that is moving through the air where the only form of acceleration acting on the object is gravitational acceleration; assuming air resistance is negligible. This is a case of projectile motion. Galileo performed quite a bit of research on projectile motion. He discovered that projectile motion takes the form of a parabola. There is a case where you won’t be able to visually see the shape of a parabola. If you were to launch a projectile at 90 degrees its flight path wouldn’t be a parabola. However, mathematically, you can still determine that the change in position in relation to velocity will be parabolic.
The study of a projectile is a two dimensional problem, where there will be equations that represents the motion of the particle in the x-direction or horizontal direction, as well as equations that represent the motion of the particle in the y-direction or vertical direction.
Horizontal Direction
First, let’s talk about the motion in the x-direction or horizontal direction. In this direction, assuming drag is negligible, there will not be an acceleration that acts on the particle, meaning that the velocity in this direction should always be constant while the position follows a linear function. Refer to the image below.
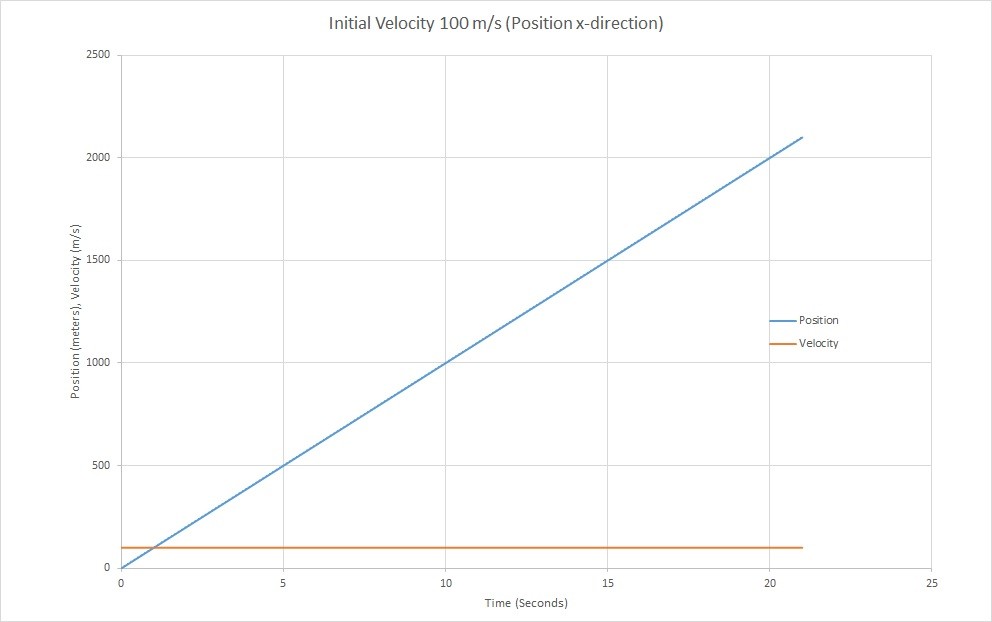
The above image represents motion of a particle in the horizontal direction for projectile motion where the initial velocity in the horizontal direction is 100$\frac{m}{s}$. Due to the fact that there isn’t any acceleration acting on the particle in the x-direction the 100$\frac{m}{s}$ velocity will be constant(which is in orange on the graph), while the position will be linear (which is in blue on the graph). You can find the position and velocity in the x-direction by using the equations below.
(Eq 1) $X(t)=V_{x_o}t+X_o$
(Eq 2) $Vx(t) = V_{x_o}$
Vertical Direction
Projectile motion is a two dimensional problem. This means that you will also need to find the motion in the vertical direction as well. For simplicity we will consider drag as negligible. In the vertical direction there is a constant acceleration due to gravity pulling the object back to earth. Due to this, the velocity in the vertical direction will be linear, while the position in the vertical direction will be parabolic. Refer to the image below. When solving a projectile motion problem you should always write the gravitational acceleration as a negative number since it direction is going down to the earth.
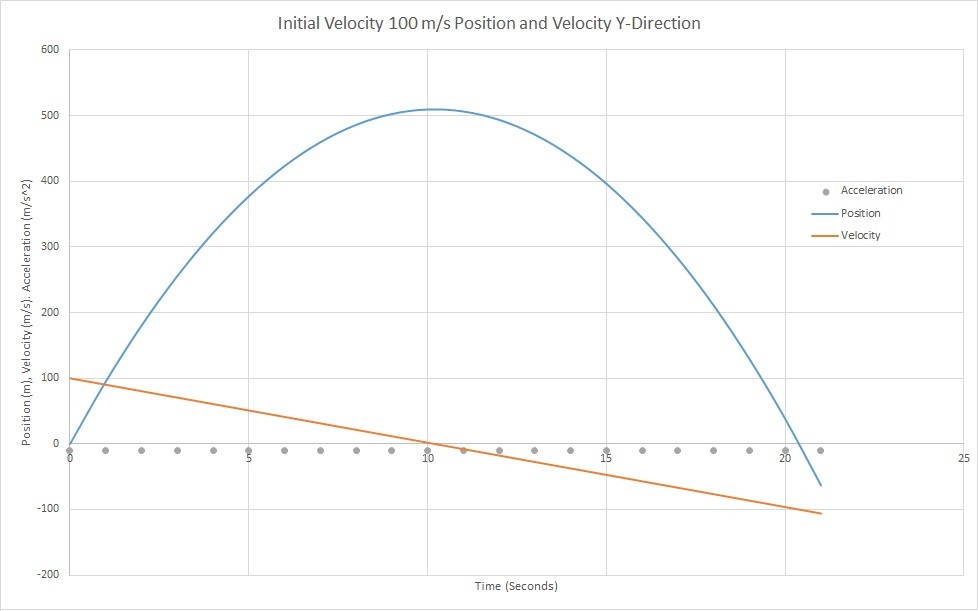
The above image represent motion of a particle in the vertical direction where the initial velocity in the vertical direction 100$\frac{m}{s}$, and the gravitational acceleration is a constant 9.81$\frac{m}{s^2}$. On the graph above the acceleration is represented by the grey dots, the velocity is represented by the orange line, and the position is represented by the blue line. Notice from the graph that the velocity in the vertical direction becomes 0 at the peak of the particles position and than becomes negative as the particle descends back to earth. This is due to the particles velocity changing direction as the position plateaus and than goes back to 0. The equations below represent the position, velocity, and acceleration of the particle in the vertical direction.
(Eq 3) $Y(t)=\frac{1}{2}g_ct^2+V_{y_o}t+Y_o$
(Eq 4) $V_y(t)=g_ct+V_{y_o}$
(Eq 5) $a_y(t) = g_c$
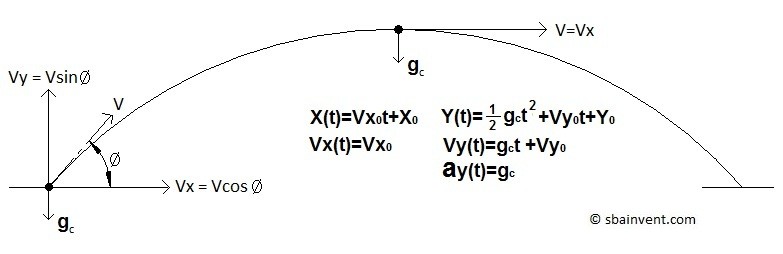
The gravitational constant on earth (g) in SI units is 9.81 m/s^2, while for British-American units it would be 32.2 ft/s^2. Below is a gneral image showing what the typical path a particle would take when subject to projectile motion.
Example
A projectile is launched at 30 degrees from the ground with an initial speed of 125$\frac{m}{s}$. Assuming the surface is completely flat and drag is negligible determine the following: total flight time, Maximum height of the projectile, the distance the projectile traveled. In addition graph the position of the projectile and velocity on the x, y plane and graph the total velocity of the projectile in respect to time.
Solution
The first step is to convert the initial total velocity into x and y components.
$V_{x_o}=125cos(30)=108.3\frac{m}{s}$
$V_{y_o}=125sin(30)=62.5\frac{m}{s}$
The next step is to determine the total flight time. Since we know the initial velocity in the vertical direction we can find the total time it will take for that velocity reach 0 meaning that the projectile has reached its total height by using equation 4. We can than multiply that value by two to find the total flight time.
$0=-9.81(t)+62.5$
$t = \frac{62.5}{9.81}= 6.37s$
$Flight~Time=2t=2(6.37)=12.74s$
Now that we know the flight time of the projectile we can find the total height the projectile traveled by using equation 3 and the distance the projectile traveled using equation 1.
Total Height (initial position is 0)
$Y=\frac{1}{2}(-9.81)(6.37^2)+62.5(6.37)=199m$
Total Distance Traveled (initial position is 0)
$X=108.3(12.74)=1380m$
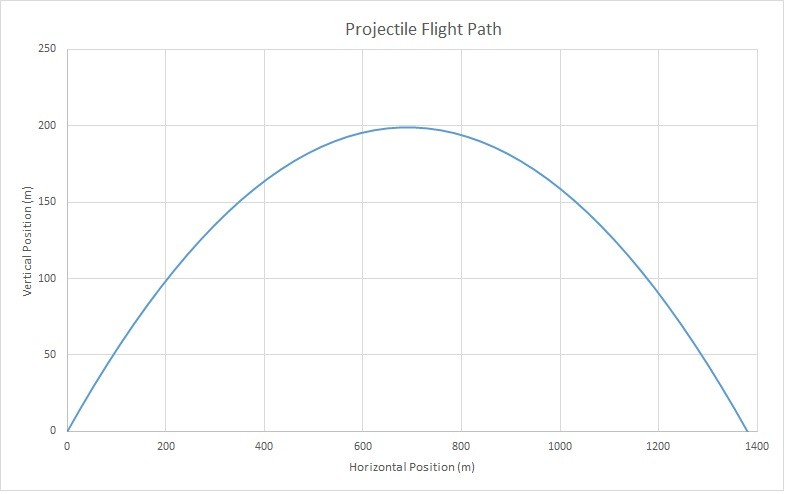
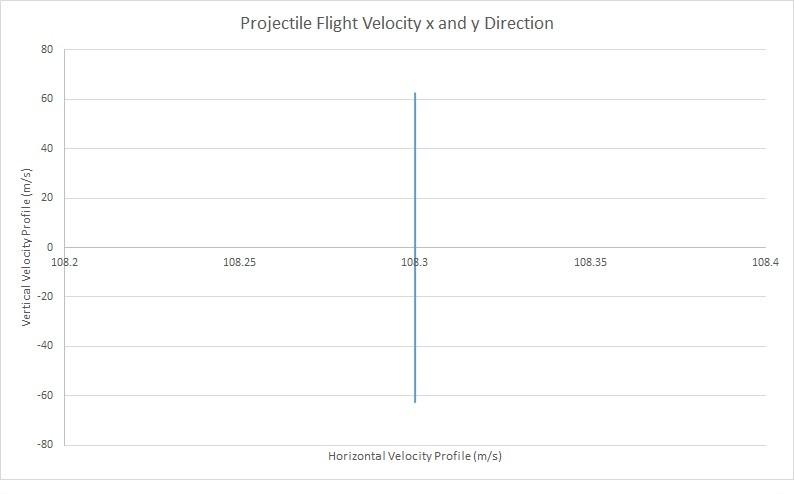
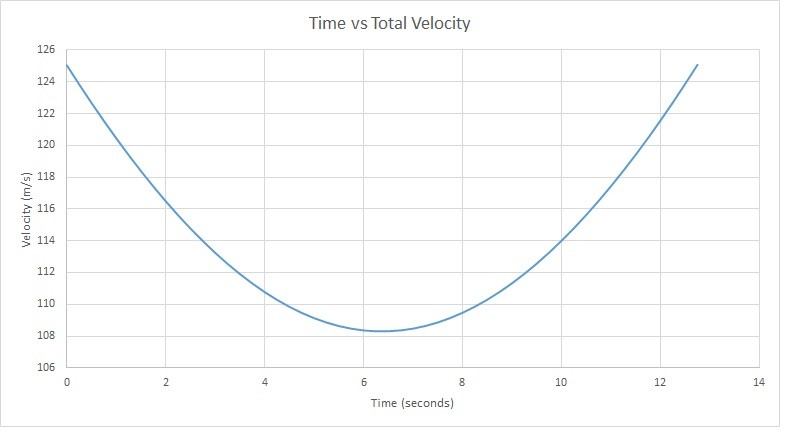
You can find total velocity by taking the magnitude of its respective x and y components.