In previous articles on displacement, velocity, and acceleration I discussed a particle that was moving in a straight line. However, what happens when the particle is changing direction through a curve? The answer is as follows.
Displacement
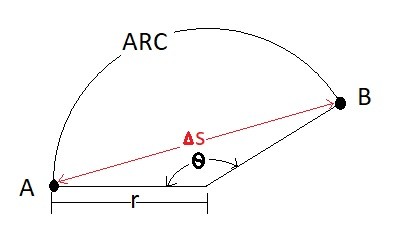
The displacement of a particle represents the change in a particles position as observed by an observer. As with particles moving in a straight line, particles that are moving around curve have their displacement observed by an observer, which means the position is subjective to that observer. However, the change is displacement is always the same regardless of who is observing the particle, as long as the observers can see an initial position and a final position. Recall for a particle moving in a straight line the mathematical equation that represents its displacement is as follows.
(Eq 1) $Δs=s′−s$
$s$ = Original Position from origin
$s′$= New position from origin
$Δs$ = Change in position
Remember that the above equation will only represent the displacement from point to point. If you want to find the arc length for a particle that is moving around a curve with a constant radius than you will need to use the following equation.
(Eq 2) $arc=θr$
Where θ is in radians
Tangential Velocity
As a particle is moving through space it will have a certain velocity that is based off how fast the displacement changes in respect to time. The equation below represents the velocity of a particle that is moving in a straight line.
(Eq 3) $v=\frac{ds}{dt}$
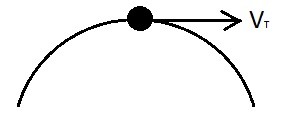
You can apply the same principles seen above to a particle that moving around a curve. As the particle moves around the curve it will have a tangential velocity. Use the equation below to find tangential velocity of a particle.
(Eq 4) $v_t=\frac{arc}{dt}$
The tangential velocity is always perpendicular to the path of a particle as it move around the corner. Let’s say that you are swinging a ball attached to rope around your head. If that rope were to break, the ball would follow a straight path that is perpendicular to the point where the rope broke. The balls flight speed will be the same speed as its tangential velocity.
Normal and Tangential Acceleration
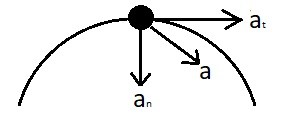
As a particle is moving around a corner it can experience two different types of acceleration. The first type of acceleration is tangential acceleration. Tangential acceleration only occurs if the tangential velocity is changing in respect to time. To find the tangential acceleration use the equation below.
(Eq 5) $a_t=\frac{v_t}{dt}$
The second type of acceleration is normal acceleration. Normal acceleration will always occur when a particle moves through a curved path. This acceleration occurs because the particle is changing direction and is there regardless of whether the tangential velocity is changing or is constant. An example in real life of normal acceleration is when you are going around corner in a car. This will result in you feeling physical force. The force that you are feeling is normal acceleration.
Normal acceleration is always perpendicular to the tangential velocity. To find normal acceleration of curved path with a constant radius you would use the equation below.
(Eq 6) $a_n = \frac{v_t^2}{r}$
You might want to find the magnitude of the normal and tangential acceleration of the particle. In order to do this you would use the equation below.
(Eq 7) $a=\sqrt{a_t^2+a_n^2}$
Example
A train is moving at 50 mph, along its route it encounters a 90 degree turn that has a radius of 75 ft. What distance does the train travel around the curve? What is the total g level felt by the passengers on the train as it goes around the curve?
Solution
What distance does the train travel around the curve?
To solve this part of the problem we need to use equation 2 and convert the 90 degrees to radians.
90 degrees = $\frac{π}{2}$ radians
distance traveled = $\frac{75π}{2}$ = 118 ft
What is the total g level felt by the passengers on the train as it goes around the curve?
To solve this problem you will have to determine what the tangential acceleration and normal acceleration are. The gravitational constant is 32.2 $\frac{ft}{s^2}$.
Tangential Acceleration
The tangential velocity is constant which means there is no tangential acceleration.
Normal Acceleration: Equation 6 would be used.
$a_n=\frac{50^2}{75}=33.3\frac{ft}{s^2}$
g-level=$\frac{33.3}{32.2}$=1.03g