In certain cases the motion of one particle could be dependent on the motion of another particle. For example if you had two objects connected to each other through a cord their motion would be dependent on each other. You could further this example by wrapping the cord around a pulley or a series of pulleys as seen in the image below.
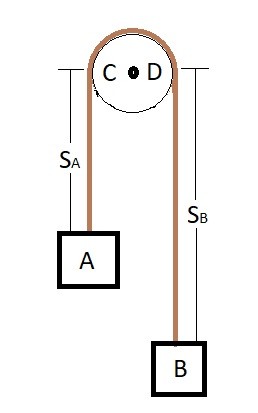
In the image above the lengths $s_A$ and $s_B$ are dependent on the positions of particle A and particle B. If you were to pull particle B down particle A will move upward. While on the other hand if you were to move particle A down particle B will move upward. This is dependent motion.
To determine how far each particle will move you will need to determine the length of the chord. You will need to find the length $S_A$ as well as the length $S_B$. Remember these two lengths will be dependent on each. To find the relationship of these two lengths use the equation below.
Eq 1 $s_A + l_{CD} + s_B = l_t$
Notice in the above equation there is a variable $l_{CD}$. This represents the length of the cord that is making contact with the pulley. A pulley will normally always have a constant diameter, which mean $l_{CD}$ will not change. You can simplify equation 1 by removing $l_{CD} from equation 1.
Eq 2 $s_A + s_B = l$
Next, if you want to find the the velocity of the two particle you will need take the derivative of equation 2 in respect to time. Realize that the the length of cord does not change in respect to time, so you will not need to include that in the equation. Refer to the equation below.
Eq 3 $\frac{ds_A}{dt}+\frac{ds_B}{dt}=0,~or~v_B=-v_A$
The negative sign in the equation above will represent a downward motion while a positive sign represents an upward motion. This means that if $v_A$ is negative than particle A will be moving downward while particle B is moving upward.
Finally, you can find the acceleration of the two particles by taking the derivative of equation 3 or the double derivative of equation 2 in respect to time. This would result in the equation below.
Eq 4 $a_B=-a_A$
For equation 4 if particle A’s acceleration shares the same direction as its velocity than the particle is accelerating, if the signs are opposite than the particle is decelerating. Also, if one particle is accelerating than the other particle is also accelerating, while if one particle is decelerating than the other particle also has to decelerate.
Example
For the image below derive the corresponding displacement equation, velocity equation, and acceleration equation.
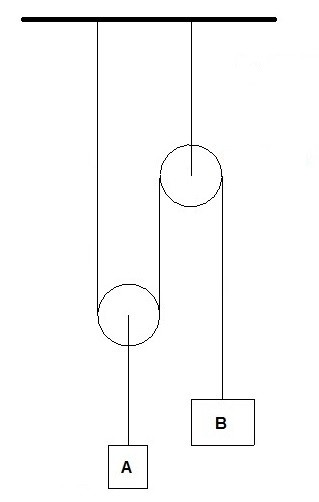
Solution
First, you will want to modify the above image to the following.
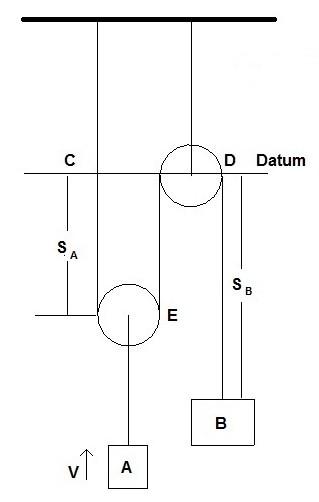
The lengths of cord that will change are between point CE, ED, and DB. CE and ED will have the same length $s_A$, while DB will have a length of $s_B$. The length of cord will not change between points A and E. You will not need to include this length of cord in the dependent motion equation.
Displacement Equation
$2s_A+s_B=l$
Velocity Equation
$2v_A+v_B=0$
Acceleration Equation
$2a_A+a_B=0$