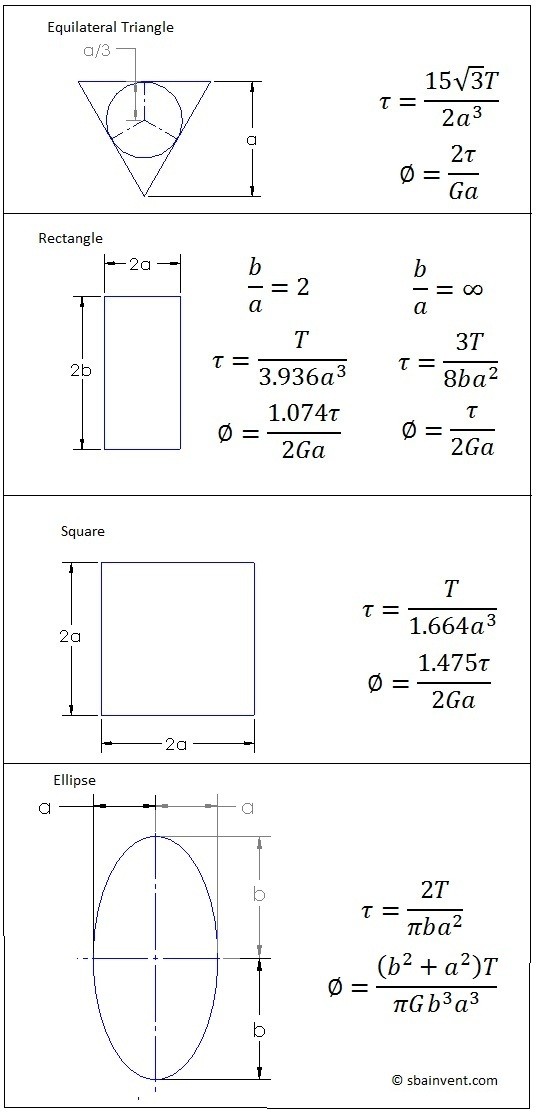
Torsional stress is much more difficult to calculate when the cross-section is not circular. Below I show how to calculate the torsional stress and angle of twist for an equilateral triangle, rectangle, square, and ellipse. However, there can be many more cases where you will have to derive these equations on your own.
Narrow Rectangular Cross-Sections
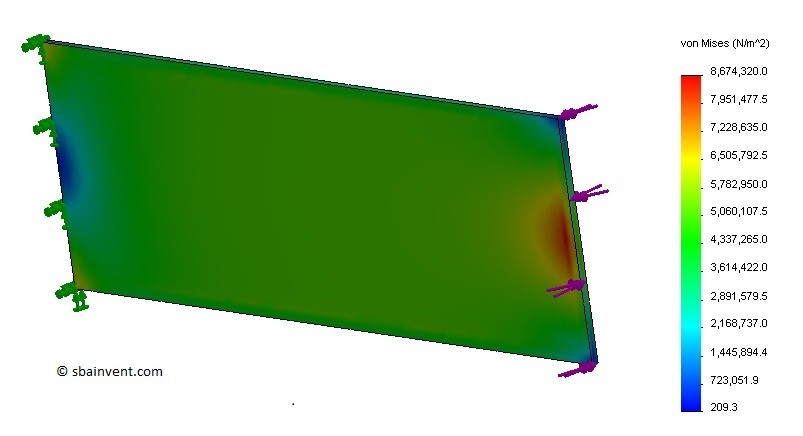
A narrow cross-sectional beam is a rectangular beam that has a width that is much greater then its thickness. Since the cross-section is not circular the stress will vary on the outside. Which can be seen in the stress profile below. Notice also that the higher stress concentration is located at the end in the center where there would normally be zero stress for a circular profile.
(Eq 1) $τ_{max}=\frac{2Ta}{J}$
$τ_{max}$ = maximum shear stress
$T$ = torque
$J$ = Polar Moment of Inertia
(Eq 2) $Φ=\frac{T}{GJ}$
$Φ$ = angle of twist length
$G$ = Shear Modulus
(Eq 3) $J=C\frac{1}{3}(2b)(2a)^3$
C = .91, b < 10a
C = 1,b > 10a
Rectangular Cross-Section
At some point the rectangular cross-section can no longer be considered narrow. When that happens equation 4 and 5 would be used to calculate the stress and polar moment of inertia, while equation 2 would still be used to calculate the angle of twist.
(Eq 4) $τ_{max} = \frac{T}{k_2(2b)(2a)^2}$
(Eq 5) $J=k_1(2b)(2a)^3$
| b/a | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 6.0 | 10 | ∞ |
| $k_1$ | 0.14 | 0.20 | 0.23 | 0.25 | 0.26 | 0.28 | 0.30 | 0.31 | 0.33 |
| $k_2$ | 0.21 | 0.23 | 0.25 | 0.26 | 0.27 | 0.28 | 0.30 | 0.31 | 0.33 |
Thin Wall Cross-Sections
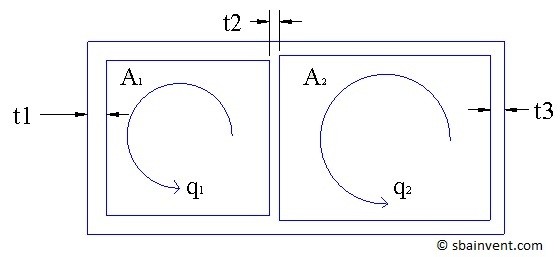
There can be cases when the object that is being studied could have multiple subsections within it; as seen in the figure below.
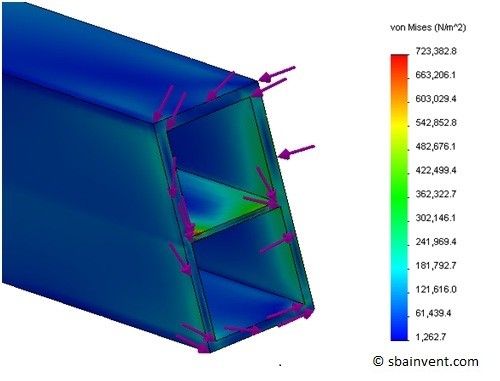
Due to these different subsections which have different wall thicknesses, the torque applied to the part will have a different effect on each section. This can be seen in the figure below.
The following equations would be used to help calculate the stress in each section.
(Eq 6) $T=2Aq=2A_1τ_1t_1=2A_2τ_2t_2=···$
$A$ = area of each section
$t$ = thickness of section wall
$q$ = shear flow
$τ$ = shear stress
(Eq 7) $J=\frac{4tA^2}{l}$
$l$ = length of each section of thickness
$J$ = Polar Moment of Inertia
(Eq 8) $Φ=\frac{Tl}{4GtA^2}$
$Φ$ = Angular of Twist
$T$ = Torque
$G$ = Shear Modulus
(Eq 9) $Φ=\frac{1}{2GA_i}\oint\frac{q_i-q’}{t}dl,~i=1,2,…,N$
what does the Ø mean in the table at the top of the page, with the shapes and the formulas?
Ø is angle of twist.