To solve a problem for unknown forces and moment statics equation are used to determine these forces. However, there are cases when there will be more unknown variables than equations to solve for them. This is an example a statically indeterminate problem. Below is an example of a statically indeterminate problem that is under torsion.
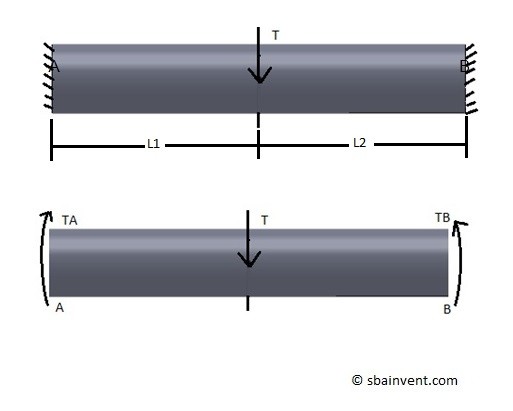
For the above problem the statics equation would be the following.
(Eq 1) $T-T_A-T_B=0$
From the resulting statics equation it can be seen that the above problem is statically indeterminate since there are two unknown variables TA and TB. In order to solve this problem another equation needs to be used. To find this equation we will need to take a look at Hook’s Law which relates stress and strain to one another. The resulting equation can be seen below.
(Eq 2) $\frac{T_AL_1}{J_1G_1}-\frac{T_BL_2}{J_2G_2}=0$
For the above problem the material is the same and so is the cross-section area which means that equation 2 can be simplified to the following.
(Eq 3) $T_AL_1-T_BL_2=0$
Next solve equation 1 for TA.
(Eq 4) $T_A = T-T_B$
The equation 4 can now be plugged into equation 3 to solve for TB.
(Eq 5) $T_B=T\left(\frac{L_1}{L_1+L_2}\right)$
Finally, we can finish solving for TA by plugging equation 5 into equation 4.
(Eq 6) $T_A=T\left(1-\frac{L_1}{L_1+L_2} \right)$