Lift
As an object is moving through a fluid it will experience a net force from the pressure field surrounding it. What causes lift force is the difference in pressure. The difference in pressure is caused by the fluids velocity going over one of the surfaces of an object faster than the opposite surface of the body. Recall from Bernoulli’s equation and continuity equation the faster the velocity of a fluid the lower the pressure and vise versa. As with drag, a lift coefficient can be used to determine the lift force; refer to equation 1.
(Eq 1) $C_L=\frac{L}{\frac{1}{2}ρU^2A}$
CL = Lift Coefficient
L = Lift Force
ρ = Fluid Density
A = Area
Recall from the drag section that there were a number of variables that could have an effect on drag. With lift, however, the most important aspect that will determine lift is the shape of the object in the fluid. The reason for this is because the shape will determine the pressure difference that causes lift.
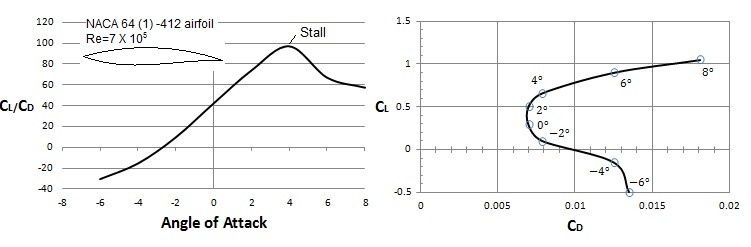
In addition to shape, the angle of attack can change how much lift an object will experience. The angle of attack is based off of the orientation of an object, such as an aircraft wing, in respect to the direction of the fluids flow. By altering the angle of attack more lift can be generated, however, if the angle of attack is to great the aircraft could stall. Refer to the figures below.
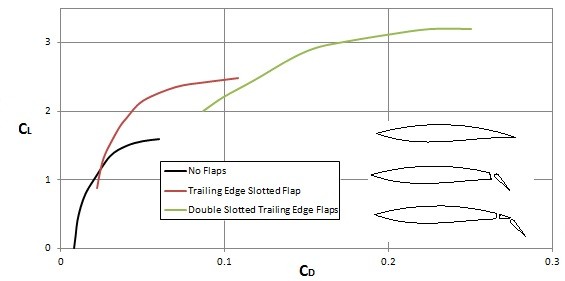
In addition to altering the angle of attack, the shape of the object or wing could be altered using flaps. For example an aircraft could extend its flaps to increase lift during takeoff, and slow speed landing. This in turn will increase drag on the aircraft, but for takeoff and landing it’s not much of a concern. This configuration is known as the dirty configuration. Once an aircraft has reach the correct speed and altitude it will retract its flaps to decrease drag for fuel economy. This is known as the clean configuration. Refer to the data below to see how flaps can affect the lift coefficient in respect to the drag coefficient.
Drag
Drag is the resistance on an object as a fluid flows past it. Different aspects can have an effect on drag such as, the objects shape, Reynolds number, Mach number, Froude number, and the roughness of the objects surface. Drag is determine by the drag coefficient. To calculate the drag coefficient equation 2 would be used.
(Eq 2) $C_D=\frac{D}{\frac{1}{2}ρU^2A}$
CD = Drag Coefficient
D = Drag Force
ρ = Fluid Density
U = Fluid Velocity
A = Area
Drag and Friction
The frictional effects due the wall shear stress as the fluid passes over an object can cause drag on an object. The orientation of the surface has a large impact on how much drag will act on the object moving through the fluid. For example if the surface is perpendicular to the upstream velocity than the shear stresses will have no influence on the drag. Also, when dealing with large Reynolds numbers the effects of friction drag could be very small in comparison to other types of drag. However, for low Reynolds number, or for shapes that are highly stream line, the main source of drag could be due to friction drag. To calculate friction drag equation 3 would be use. To use equation 2 you will need to know a friction drag coefficient.
(Eq 3) $D_f=\frac{1}{2}ρU^2bLC_{df}$
Df = Frictional Drag Force
ρ = Fluid Density
U = Fluid Velocity
b = Objects Width
L = Objects Length
Cdf = Drag Coefficient
Drag and Pressure
The pressure field created as a fluid moves over an object can also cause drag. This drag is directly related to the speed of the fluid moving over the object; the faster the fluid is moving the greater the magnitude of drag. The orientation of the surface to the flow will also have an effect on the magnitude of drag; surfaces that are normal to the flow will convert all of the pressure acting on that surface into drag, while surfaces parallel to the flow will feel very little drag effect due to the pressure field. To calculate the pressure drag refer to equation 4.
Drag Coefficient Data
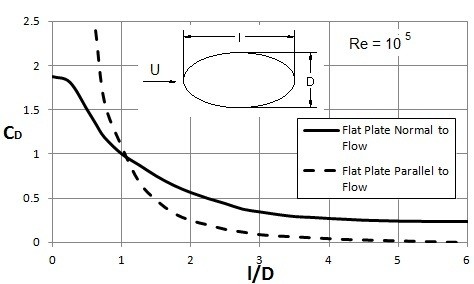
As mentioned earlier, the shape of an object can have an effect on the drag. Below is data on a flat plate that has the flow normal to the plate and the flow parallel to the plate to show how orientation can change the shape which in respect will change the drag on the object.
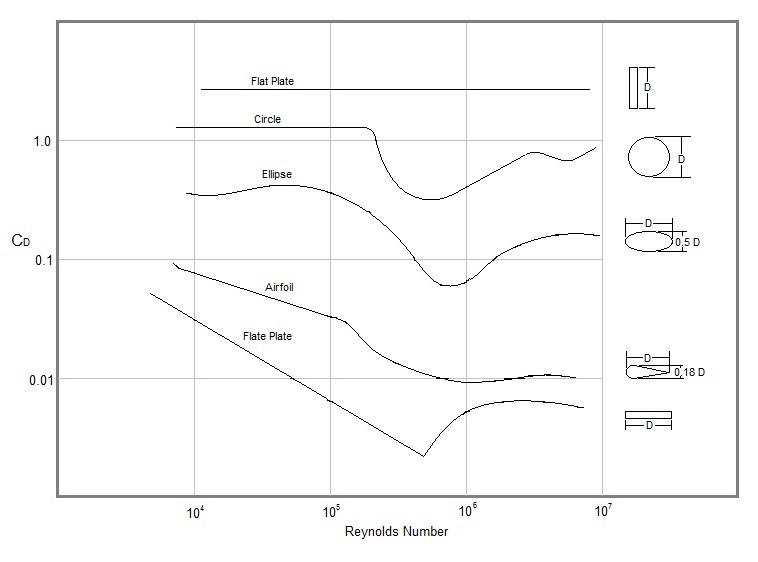
In addition to shape, Reynolds number can have an effect on the drag on an object due to the fact that as Reynolds number becomes higher the boundary layer will shift from a laminar flow to a turbulent flow. Refer to the data below to determine the drag coefficient for a variety of situations.
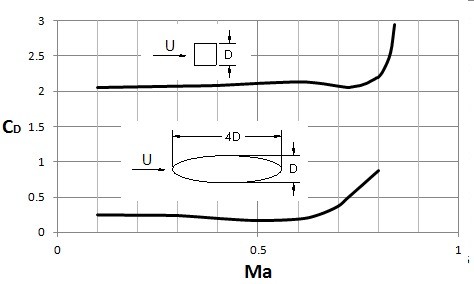
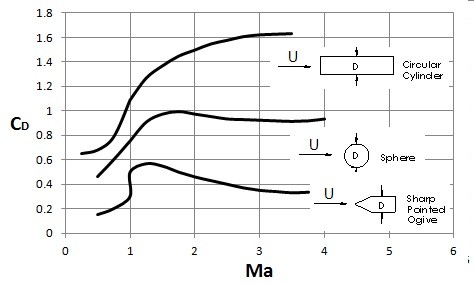
Also, the Mach number has influence on the drag on an object due to the fact that it can be used to determine the influence of the fluid compressibility factor if it is a compressible fluid. Typically if the Mach number is below 0.5 then the compressibility of the fluid can be considered negligible, however as the Mach number passes that value the compressibility factor becomes more influential. Refer to the data below.
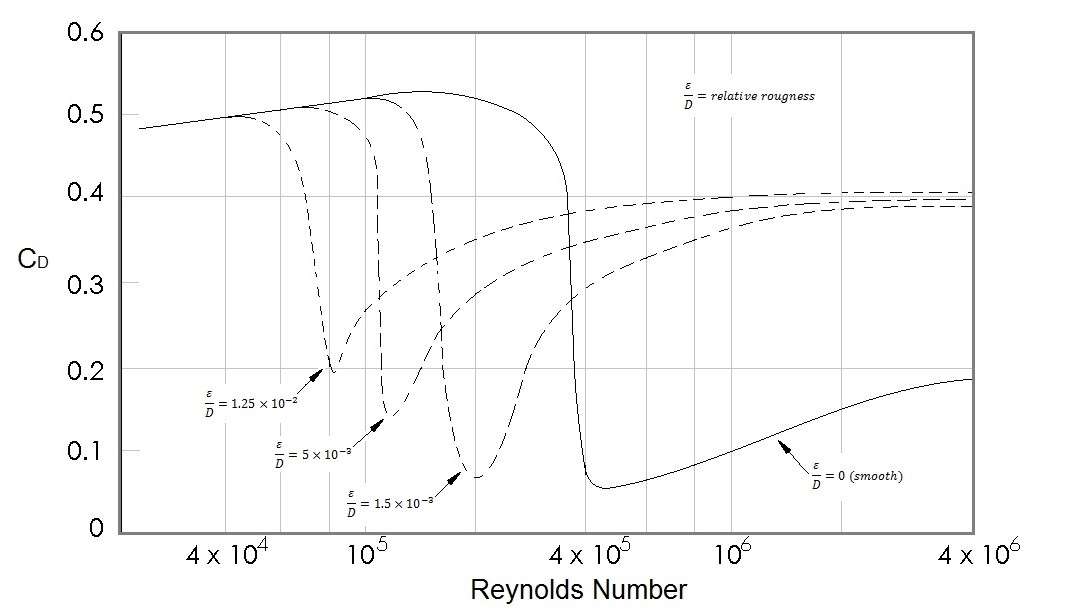
Finally, surface rough can have an influence on drag, especially in the turbulent area of the boundary layer. Refer to the data below to see the roughness effects on a sphere.
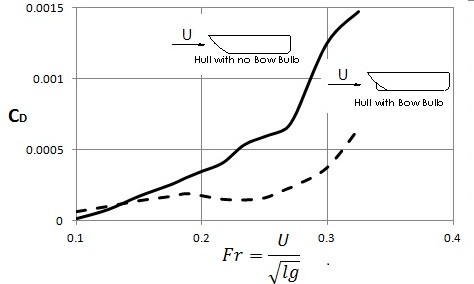
Froude Number
Froude number is used to determine the drag effects caused by the waves produced by ships. What Froude number does is it takes ratio of the free-stream speed to a typical wave speed on the interface of two fluids. Depending on how a ship or some other object moves through the water, different types of waves will be produced. If the drag effect on the waves is larger than say another set of waves produced by another ship, then the ship that produced the first set of waves is using more energy than the other ship since it takes energy to create the waves. Refer to the data below to view the difference between two different types of ship hulls.