As an object moves through fluid, or when a fluid moves over a stationary object, there will be a net force that is in the direction of the flow. This force is known as drag. This force is created by the pressure and shear forces on the on the surface of the immersed body. Most information that is known today about drag has been obtain experimentally through the use of wind tunnels, towing tanks, and water tunnels. As a result, through these experiments we are able to determine the drag coefficient $C_D$ which can than be used to analytically determine the drag on similar shapes.
(Eq 1 ) $C_D=\frac{D}{\frac{1}{2}ρU^2A}$
$ρ$ = fluid density
$D$ = drag
$U$ = fluid velocity
$A$ = the frontal area
In addition, drag is a function of the following dimensionless parameters, Reynolds Number, Mach Number, and Froude Number, as well as the relative surface roughness of the object.
(Eq 2) $C_D=Φ(shape,~Re,~Ma,~Fr,~ε/l)$
$ε$ = surface roughness
$l$ = length
Friction and Pressure
There are two variable that will effect drag. They are friction and pressure.
Drag Friction
Friction is directly related to shear stress as well as the orientation that the fluid interacts with the surface of the object. For example, a flat plate that is parallel to the flow, the entire shear force will contribute directly to drag. On the other hand, if the plate is perpendicular to the upstream velocity the shear force does not contribute to drag. Generally, most objects will have surfaces that are perpendicular and parallel to the flow. An example of such body is a circular cylinder.
For most fluids, the contribution of drag caused by friction will be relatively small since the viscosity of most common fluid is small. This is because Reynolds number of most flows is relatively large. When this occurs pressure is more influential. However, for a low Reynolds number flow friction will be more influential. To determine drag caused by friction on a flat plate the following equation would be used.
(Eq 3) $D_f=\frac{1}{2}ρU^2blC_{Df}$
$C_{Df}$ = friction drag coefficient
$b$ = plate width
drag Pressure
Pressure on the object can also cause drag, which is sometimes referred to as form drag. The reason for this is because this drag is directly depended on the shape or form of the object of interest. It is also a function of the orientation of the object in relation to the upstream velocity. For example, even though pressure on either side of a flat plate could be large it will not contribute to the drag if the plate is parallel to the flow. On the other hand, if the pressure on the plate is normal to flow than that pressure will contribute completely to drag. To determine pressure drag the following equation would be used.
(Eq 4) $D_p=\int{}p~cos~θ~dA$
$p$ = pressure
Taking the pressure drag coefficient $C_{Dp}$ into consideration the above equation can be rewritten as the following.
(Eq 5) $C_{Dp}=\frac{D_p}{\frac{1}{2}ρU^2A}$$=\frac{\int{}p~cos~θ~dA}{\frac{1}{2}ρU^2A}$$=\frac{C_p~cos~θ~dA}{A}$
Where $C_p=(p-p_o)/(ρU^2/2)$ is the pressure coefficient. $p_o$ is the reference pressure. The reference pressure does not directly influence the drag since it will be cancelled out by the net pressure forces.
Shape Dependence
The shape of the object has a major impact on the drag coefficient of that object. Shapes can range from streamline to blunt. In turn, typically the more blunt an object is the higher the drag coefficient. On the other hand, a streamline object will have a low drag coefficient. The image below shows how drag coefficient will change for an ellipse as the aspect ratio $l/D$ changes. $D$ and $l$ are the thickness and length of the plate.
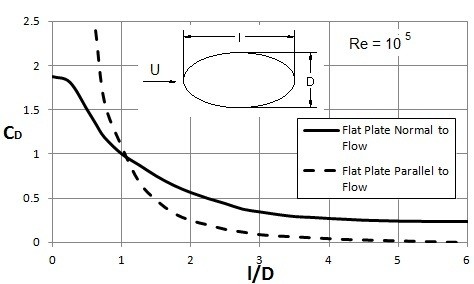
In the image above if the aspect ratio, $l/D=0$, than the ellipse will behave like a flat plate that is normal to the flow. On the other hand, if the aspect ratio becomes very large, $l/D=∞$, the ellipse will behave like a flat plate that is parallel to the flow. When this is the case the friction drag will be greater than the pressure drag. For bodies that are extremely thin, the drag coefficient is defined using the planform area $A=bl$. The reason why the planform area is used is because it is the area on which the shear stress acts. For an ellipse the planform area’s drag coefficient can found using the following equation.
(Eq 6) $C_D=\frac{D}{ρU^2bl/2}$
Reynolds Number
In addition to shape, the drag coefficient is also dependent on Reynolds number. There are three categories of Reynolds number dependency. They are low Reynolds number, moderate Reynolds number, and high Reynolds number.
Low Reynolds Number
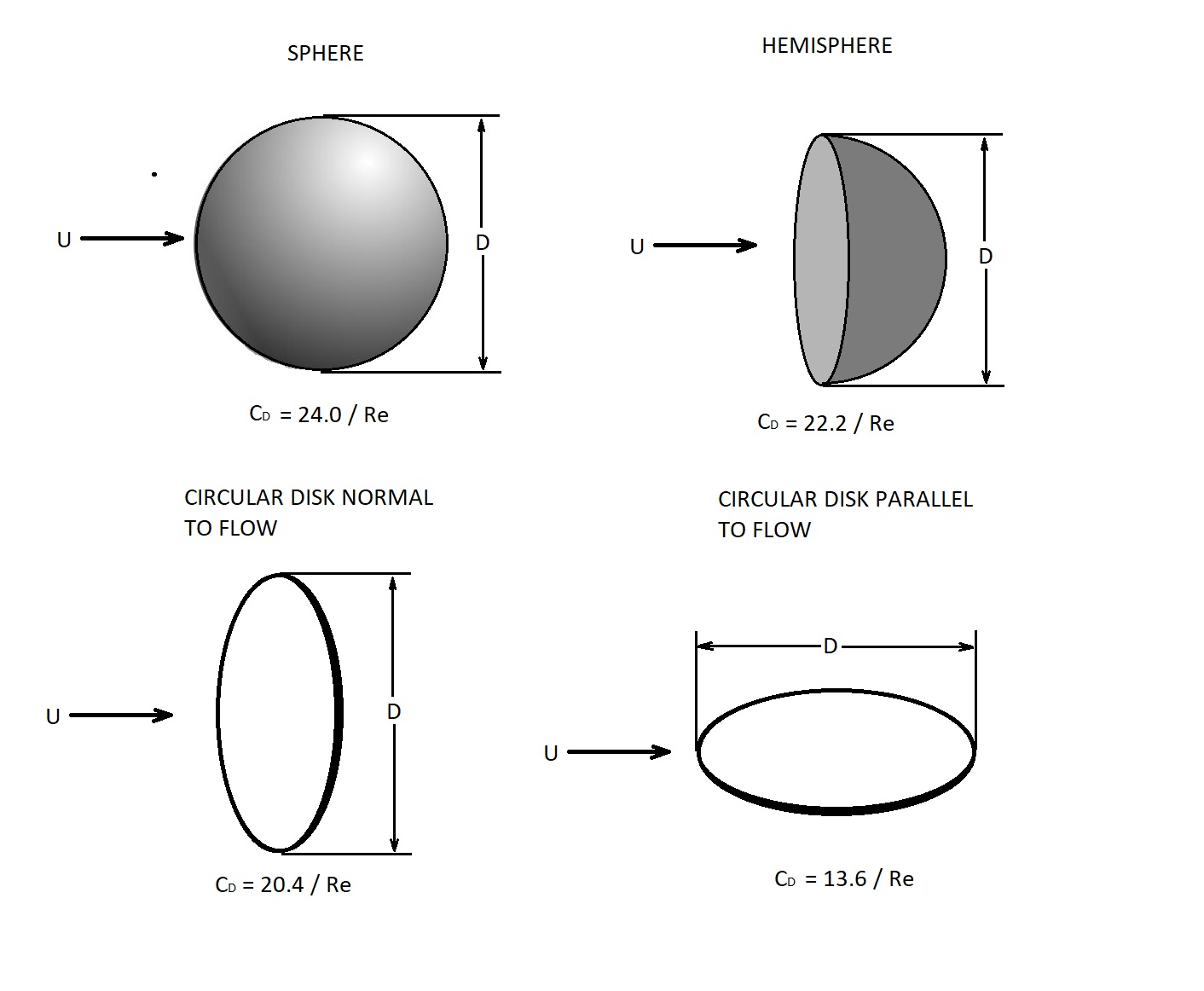
A low Reynolds number is defined as $Re<1$. In this case the viscous and pressure forces are prominent while inertial effects are negligible. Due to this fact the drag on a three-dimensional body will be a function of the upstream velocity, $U$, the size of the body,$l$, and the fluids viscosity, $μ$. Or
(Eq 7) $D=f(U,~l,~μ$
From a dimensional consideration this will become.
(Eq 8) $D=CμlU$
In this equation $C$ is dependent on the shape of the body. Finally, equation 8 can be put into the following dimensionless form.
(Eq 9) $C_D=\frac{D}{\frac{1}{2}ρU^2l^2}=\frac{2CμlU}{ρU^2l^2}=\frac{2C}{Re}$
The following image shows the drag coefficient for some basic shapes for low Reynolds number.
Moderate Reynolds Number
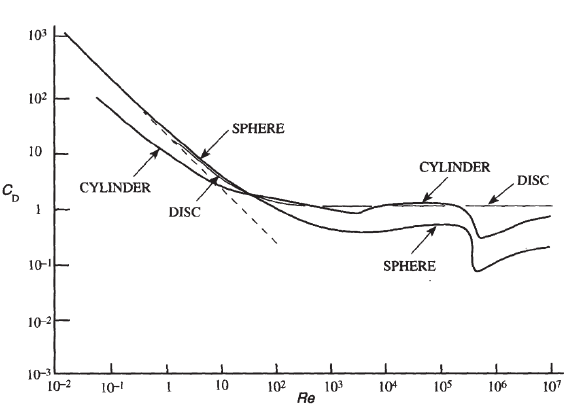
A moderate Reynolds occurs between $10^3<Re<10^5$ for blunt objects such as spheres and circular cylinders. At this point the flow has formed a boundary layer structure. However, for any given object there will be a wide variety of flow situations that could occur. In addition, when the boundary layer becomes turbulent there will be a sudden change in character of the drag coefficient. This a function of the shape of the body. Finally, if the body is streamline the drag coefficient will increase. This is because most of the drag on the body is due to shear stress which increases when the flow is turbulent. The following images show how the drag coefficient is effected from a change in Reynolds number as well as the shape of the object.
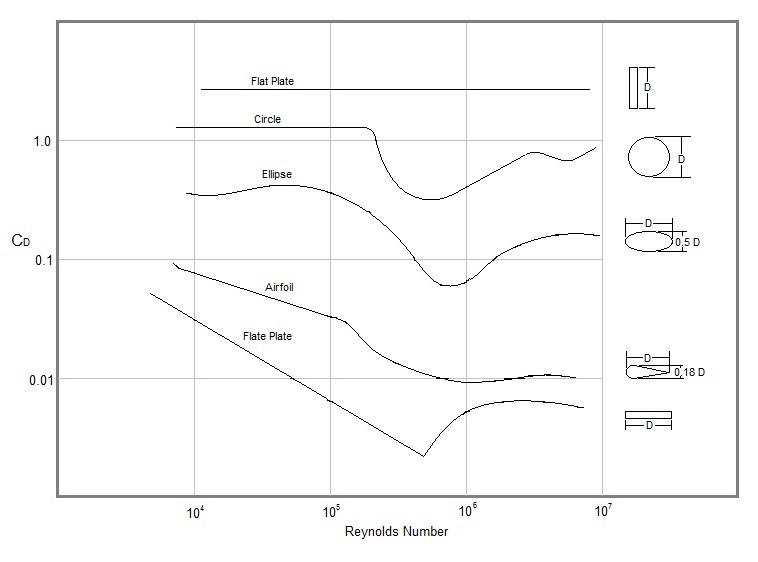
Compressibility Effects
Up to this point I have restricted the discussion to incompressible flow. However, for a gas, when the fluid velocity becomes significantly large than compressibility effects must be considered. As a result, the drag coefficients will become a function of the Mach Number, $Ma$.
(Eq 10) $Ma=\frac{U}{c}$
$c$ = speed of sound through the fluid
Having to consider the Mach number, in addition to Reynolds Number, complicates things. This is because it is difficult to determine how much either the Mach number or the Reynolds number contribute to the drag coefficient. However, there are certain simplifications that can be used to make this easier. For instance, if the Mach number is low, $Ma<0.5$, the compressiblity effects can be considered unimportant. However, for a high Mach number, the drag coefficient will be strongly dependent on the Mach number, while Reynolds number will have only secondary effects. Finally, the drag coefficient will increase significantly within the vicinity of $Ma=1$. This can be seen in the image below.
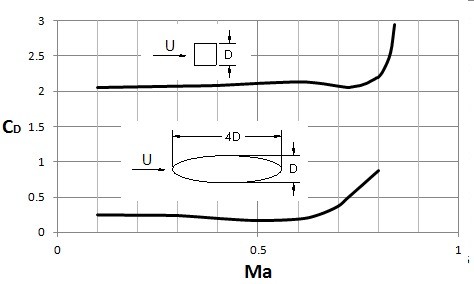
The reason why the drag coefficient increases so significantly is due to the formation of shock waves. A shock wave is an extremely narrow region within the flow field. In this region the the flow parameters will change in a nearly discontinuous manner.
Once an object moves past $Ma=1$, or reaches super sonic speeds, the drag coefficient will level off or start to decrease depending on the object. This can be seen in the following image.
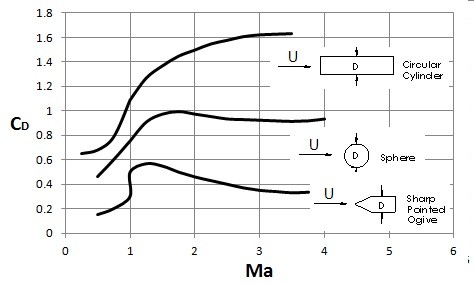
Objects that are more streamline will see the drag coefficient decrease, while objects that are blunt will not.
Surface Roughness
Surface roughness can also have a significant influence on the drag coefficient when the flow is turbulent. The reason why is because the surface roughness will increase turbulent shear stress. It can also alter the Reynolds number at which the flow will become turbulent. For example a flat plate that is rough will have a larger portion of length that is turbulent compared to an identical plate that is smooth.
For streamline bodies surface roughness is more of concern. As a result, when airplanes wings are designed great care is taken to make the wing as smooth as possible. On the other hand, for extreme blunt objects, drag will be independent of surface roughness. In fact for spherical and circular cylindrical objects, an increase in surface roughness can actually decrease drag. The image below shows how the drag coefficient is effected for various surface roughness.
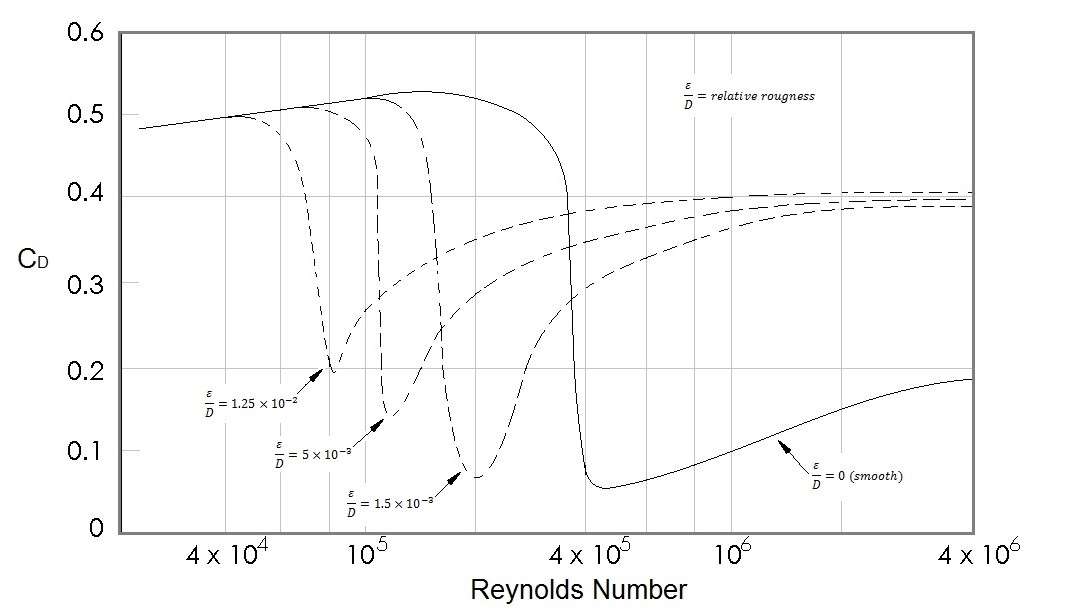
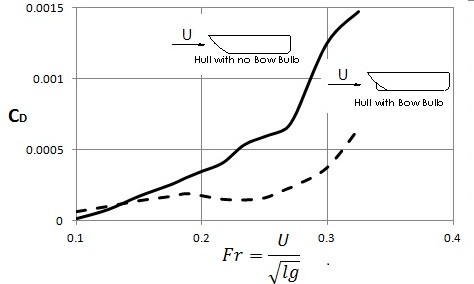
Froude Number
The Froude,$Fr$, number is a ratio of the free-stream speed to a typical wave speed at the interface of two fluids. An example of this would the surface of the ocean.
(Eq 11) $Fr=\frac{U}{\sqrt{gl}}$
Where Fronde number is most useful is determining the drag on a ship as it moves through the water. This is because as a ship moves through the water it will produce waves. These waves require a source of energy to be generated which will cause drag on the ship. This can be a complex function of the Froude number and the body shape of the ship. To determine the wave-making drag coefficient the following equation is used.
(Eq 12) $C_{DW}=\frac{D_w}{ρU^2l^2/2}$
The following image can be used to determine the wave-making drag coefficient for a hull with no bow bulb and a hull with a bow bulb. However, this image presents an example, and experiments should be conducted on different unique designs to determine the actual drag coefficient for that unique shape.