When a fluid moves over an immersed body there will be a resultant force. This is because of the external flow characteristics causing an interaction between the body and the external fluid. In turn, this will happen for cases when the body is moving through the fluid as well as when the fluid is moving over the the body. In either case we would normally state that the body is stationary by fixing a coordinate system to the body. As a result, this will make the body appear to be stationary allowing us to say that the fluid is flowing past the body at a velocity $U$. The fluid velocity is called the upstream velocity. For simplicity, the upstream velocity will be uniform and constant. In reality this statement is normally not true.
In a real world situations the flow will be unsteady. Even if the flow is for the most part uniform, at the vicinity of the object the flow will become unsteady. For example, during a windy night as the air flows past power lines on a telephone pole the wind will whistle. This whistling noise is be created by irregular turbulent fluctuations in the wake behind the body.
When you are analyzing a body there are three general categories. The first category is two-dimensional objects that are infinitely long with constant cross-section. In reality there is no such thing as a two-dimensional body. However, some objects are significantly long that the end effects are negligible. The second category is asymmetric bodies. Asymmetric bodies are formed by rotating a cross-sectional area around an axis of symmetry. Finally, the third category are three-dimensional bodies. These three-dimensional bodies could have a plane or axis of symmetry but they may not as well.
Lift and Drag of an External Flow
As stated above, as a body moves through a fluid there will be a resultant force. This force is either creates lift or drag on the body. In turn, these forces can also be described as a stresses because they are caused by the wall shear stress $τ_w$. The wall shear stress is caused by viscous effects of the fluid as well as normal stresses caused by the pressure $p$.
As stated above the resultant forces will cause either a lift $L$ or a drag $D$. Lift is the resultant force that is normal to the upstream velocity. On the other hand drag is the result force that is in the direction of the upstream velocity. This can be seen the following image.
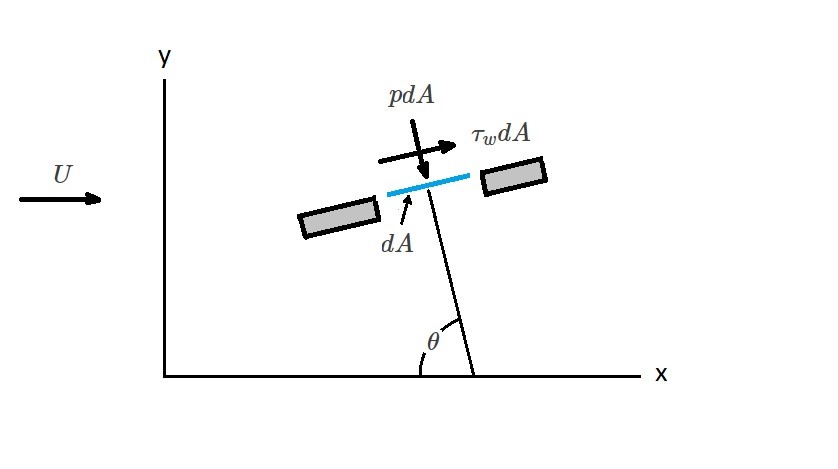
From this image we can determine the force in x-direction by using the following equation.
(Eq 1) $dF_x=(p~dA)~cos~θ+(τ~dA)~sin~θ$
In addition, the force in the y-direction is found using this equation.
(Eq 2)$dF_y=-(p~dA)~sin~θ+(τ~dA)~cos~θ$
Next, the lift and drag components can be found by determining the net x and y components of the force.
(Eq 3) $D=\int{}~dF_x=\int{}p~cos~θ~dA+\int{}τ_w~sin~θ~dA$
and
(Eq 4) $L=\int{}~dF_y=-\int{}p~sin~θ~dA+\int{}τ_w~cos~θ~dA$
Realize that you must know the shape of the body to perform these integrations. You will also need to know what the wall shear stress distribution is as well as the pressure on the surface of the body. It can be quite difficult to obtain the pressure distribution as well the wall shear stress. The pressure distribution can be determine experimentally by using static pressure taps along the bodies surface. However, it is very difficult to measure wall shear stress. Note for most bodies shear stress and pressure contribute to both lift and drag. This is because arbitrary body angle is neither zero or $90^o$ with the exception of a flat plate that is either parallel of upstream to the flow.
Lift and Drag Coefficients
Now since equations 3 and 4 are difficult to use, experimental data has been collected through the years to develop lift and drag coefficients for certain shapes and flow situations. The equations for the lift coefficient, $C_L$, and the drag coefficient, $C_D$, can be seen below.
(Eq 5) $C_L=\frac{L}{\frac{1}{2}ρU^2A}$
$ρ$ = fluid density
and
(Eq 6) $C_D=\frac{D}{\frac{1}{2}U^2A}$
In these equations $A$ represents the frontal area. The frontal area is the projected area seen by the a person looking at an object. This person must be looking at the object in a direction that is parallel to the upstream velocity.
Flow Characteristics Around an Object
How a fluid moves around a body is a function of the shape of the object. As a result, simple shapes, such as spheres, will have a less complex flow profile than more complex shapes. However, even simple shapes can produce a complex flow.
There are a number of variables that will effect how a fluid will flow around an object. For instance, size, orientation, speed, as well as the fluid properties will determine how the fluid flows around an object. To help consolidate these various parameters dimensional analysis is used. In turn, various dimensional parameters will result. However, the most important dimensional parameters are Reynolds number,$Re$, Froude number,$Fr$, and Mach number,$Ma$.
(Eq 7) $Re=\frac{ρUl}{μ}$
$l$ objects length in the direction of the flow
$μ$ = dynamic viscosity
(Eq 8) $Ma = \frac{U}{c}$
$c$ = speed of sound of the fluid
(Eq 9) $Fr=\frac{U}{\sqrt{gl}}$
$g$ = gravitational constant
Reynolds Number: Characteristics of an External Flow
Out of these three parameter, I will mainly be focusing on how Reynolds number effects the characteristics of an external flow. In order to calculate the Reynolds number you will need know what the objects length is as well as what the fluid’s velocity is. Generally, a moderately sized object will have length that is $0.01 m < l < 10 m$, while the fluids velocity will be$ 0.01 m/s < U < 100 m/s$. As a result, the Reynolds number will be somewhere between $10 < Re <10^9$. Of course, these values are just a statement, and you may have situations that fall outside of these ranges.
Now what is Reynolds number? Reynolds number is a ratio between the inertial effects and the viscous effects. As a result, depending on what the value of Reynolds number is will determine if the viscous or inertial effects are more influential. Normally, if $Re>100$ than the flow is dominated by inertial effects. On the other hand, if $Re<1$ the flow is dominated by viscous effects. This is important because it will effect how a fluid will flow around the object. The images below illustrate the a fluid will flow around a flat plate for different Reynolds numbers. In these images you will notice that the area effected by the viscosity decreases as the Reynolds number increase.
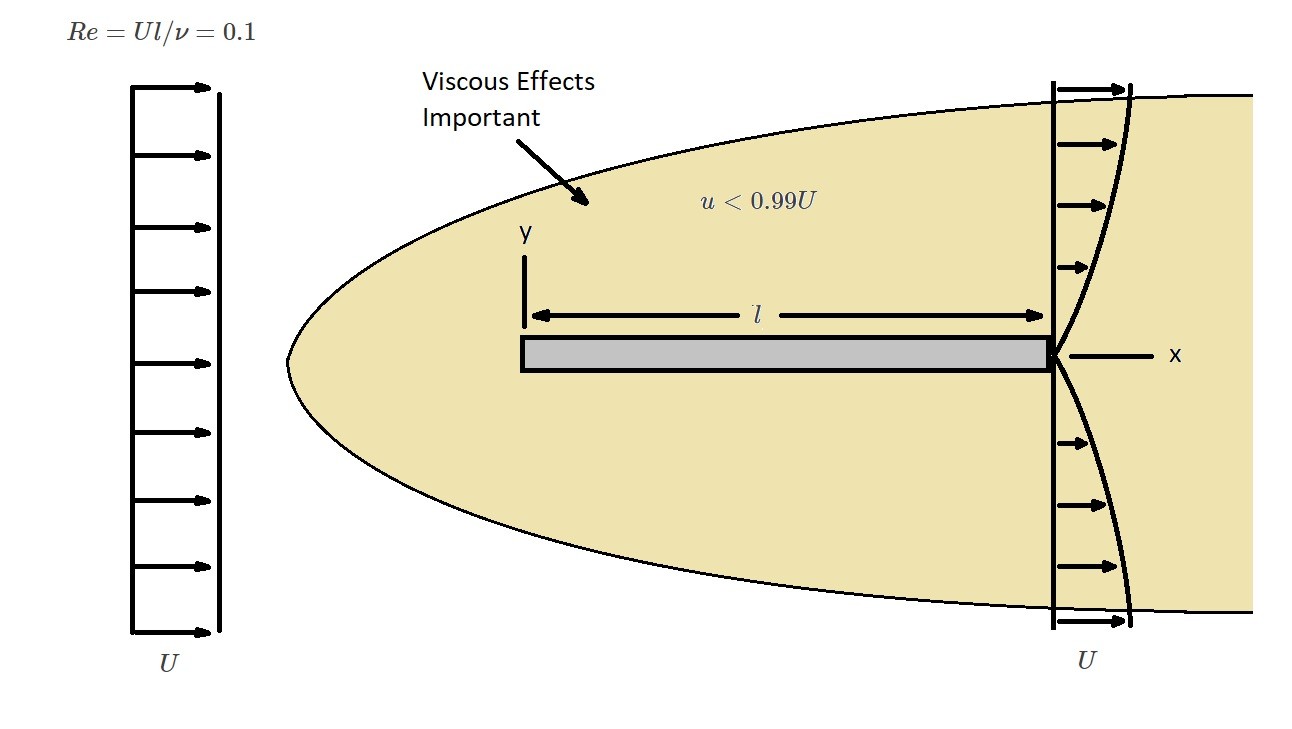
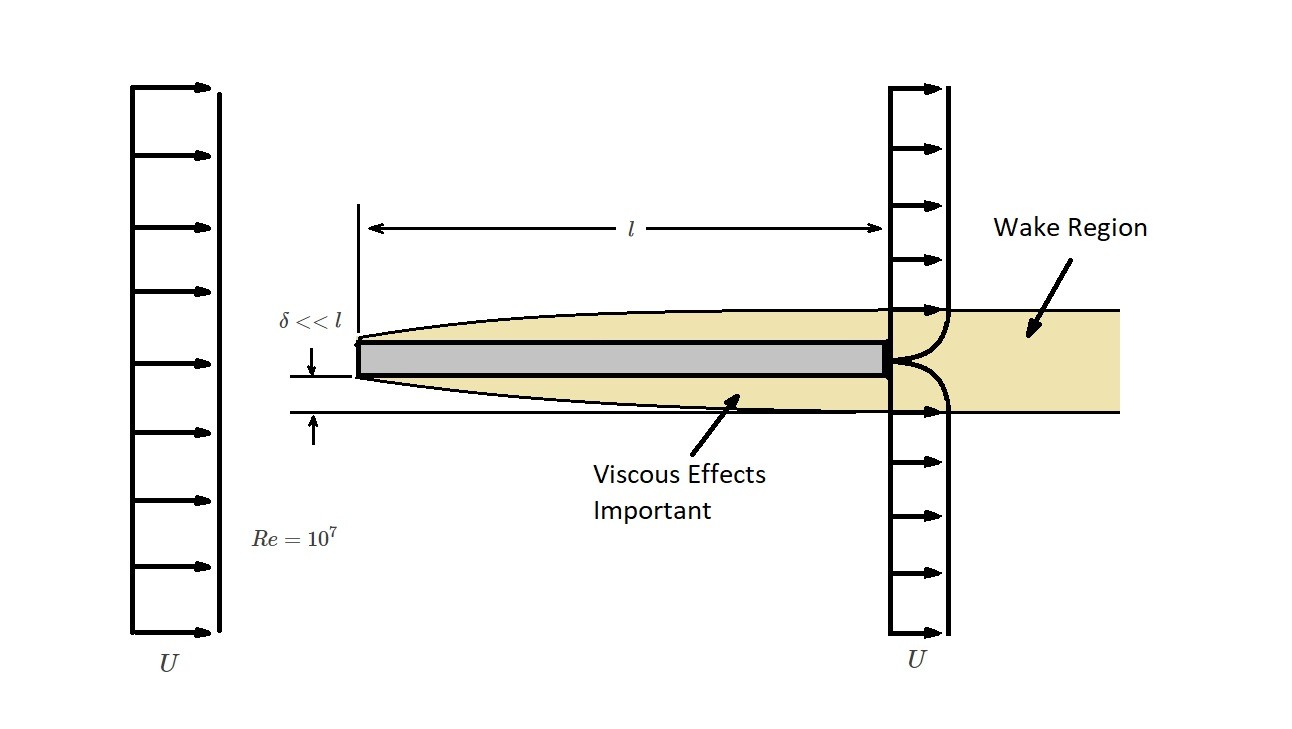
From these images it can be seen that for a large number the flow is dominated by inertial effects. In turn, this causes the viscous effects to be negligible except very close to the plate and within the wake region.
The area where the viscous effects is noticeable is called the boundary layer. As the fluid moves over the plate the fluid will stick to the plate due to viscous forces. In turn, the fluid particles will also stick to one another. As a result, the fluid velocity at the plate will zero and will increase the further the fluid particles are from the plate until they reach $u=U$. In addition, the boundary layer thickness is $δ=δ(x)=<<l$. From this statement, we can conclude that the boundary layer is relatively thin in comparison to the plate’s length. However, the boundary layers thickness will increase in the direction of the flow along the plate. The boundary thickness will zero on the lead edge of the plate.