There are infinite types of boundary layers since there is infinite types of shapes. However, for this article I am going to discuss one of the simplest boundary layers. This occurs when a incompressible, viscous fluid flows over an infinitely long flat plate.
Reynolds Number
When we are looking at this type of problem we also need to take look at the Reynolds number. As discussed in a previous article the Reynolds number will influence the boundary layer. If the Reynolds number is significantly large a thin boundary layer in relation to the plates length will result. It is important to note for an infinitely long plate it is not possible to calculate the Reynolds number since the length goes to infinity. On the other hand a finite plate will have certain length $l$. To calculate the Reynolds number of a finite plate you will use the following equation.
(Eq 1) $Re_L=\frac{Ul}{ν}$
$U$ = upstream velocity
$l$ = plate length
$ν$ = kinematic viscosity
In addition, the fluid that is not within the boundary layer will not experience the viscous effects that the fluid inside the boundary layer does. As a result, the fluid outside the boundary layer will be $V=U\hat{i}$. For an infinitely long plate, the boundary layer will take on the form scene in the image below.
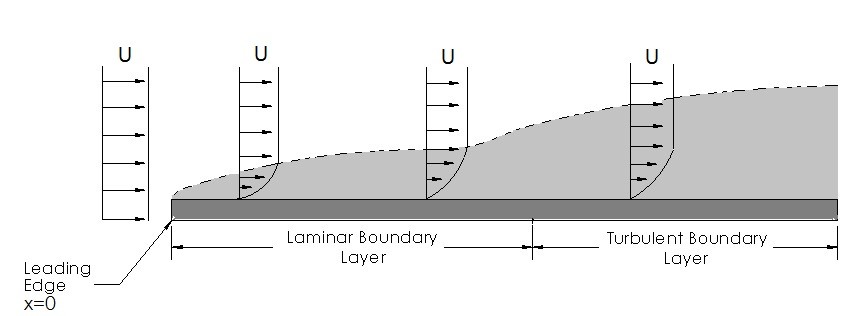
To calculate the Reynolds number for an infinitely long plate you would use the following equation. In this equation x represents the length of interest.
(Eq 2) $Re_x=\frac{Ux}{ν}$
As a result, a significantly large plate will produce a sufficiently large Reynolds number. As the Reynolds number becomes larger the boundary layer will become more pronounced the further it is from the leading edge.
Flow Characteristics
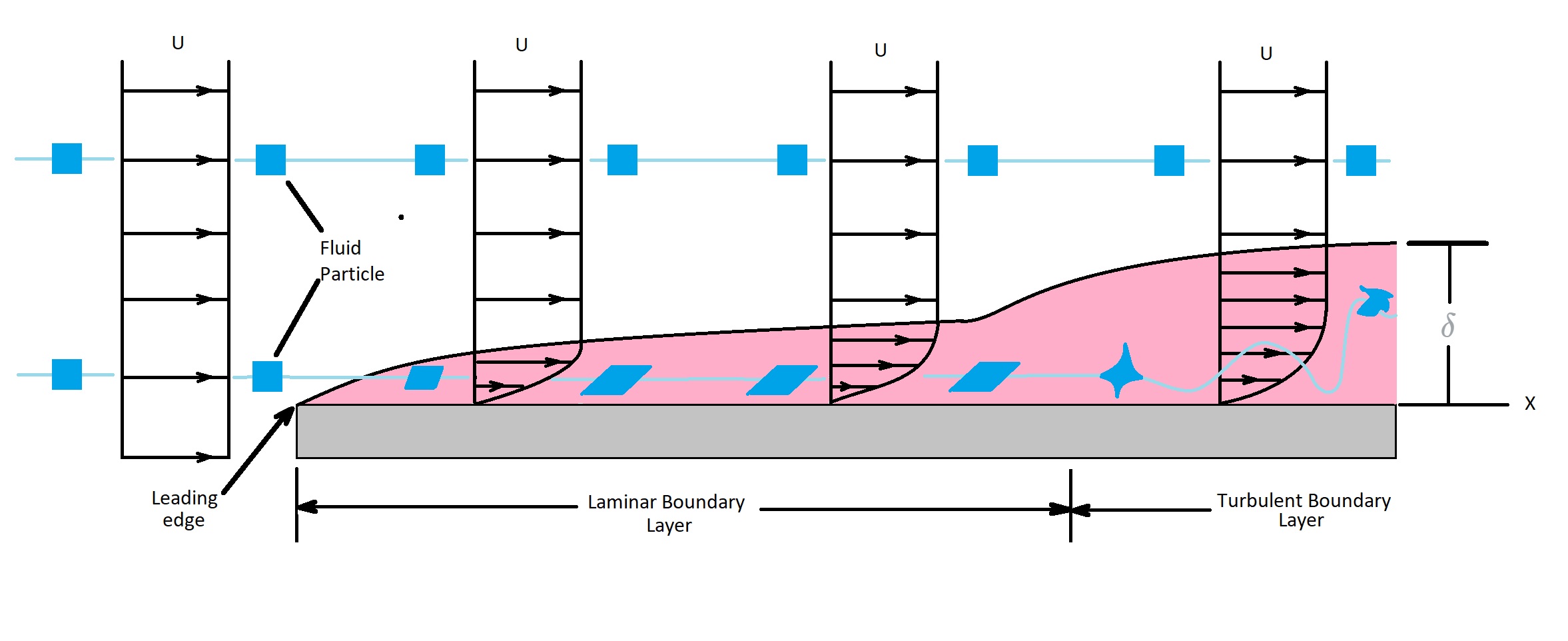
To understand how a fluid flows over a flat plate we will need to take a look at the individual fluid particles. First, any fluid particles outside the boundary layer will have a uniform flow. However, once a fluid particle enters the boundary layer things begin to change.
Let’s say that fluid particle takes on the shape of a perfect square that occupies a finite area. Outside of the boundary layer the square will always look like a square since the flow is uniform. However, once the fluid particle enters the boundary layer that square will start to distort. This distortion is due to the velocity gradient within the boundary layer. This means that the top of the square will have a greater fluid velocity than the bottom of the square causing it to distort. Finally, due to the viscous flow within the boundary layer the particle will begin to rotate. It will not rotate outside of boundary layer.
In addition, as the fluid flows over a the plate it will at some length enter a turbulent state of flow. When this occurs the fluid particle will become greatly distorted. It will also have an random irregular flow. In turn, this will cause a mixing of particles, which is beneficial for certain applications like Heat Transfer. The transition from laminar flow to turbulent flow will occur when the Reynolds is $2×10^5$ to $3×10^6$. The actual transition is dependent on the roughness of the plates surface as well as the amount of turbulence within the upstream flow.
Boundary Layer
The Boundary Layer is used to describe how the fluids velocity will change from the upstream velocity $U$ to zero velocity on the surface of the plate. In other words, $V=0$ at $y=0$, where $y$ represents the surface of the plate. In addition, $V≈ U\hat{i}$ at the edge of the boundary layer. Hence, the velocity profile $u=(x,y)$ will bridge the boundary layer thickness. The boundary layer thickness layer thickness $δ$ represents the distance from the surface of plate in which the fluid velocity is with some arbitrary value of the upstream velocity.
(Eq 3) $δ=y$ where $u=0.99U$
This statement holds true for a variety of shapes and sizes and is not used only on a infinitely long flat plates.