As fluid flows over a submerged object a boundary layer is formed. The boundary layer is due to the shear stress caused by the viscous effects of the fluid as it moves over the object. Depending on the length of the object and the speed of the fluid, the boundary layer could exhibit both laminar and turbulent flow. Refer to the figure below.
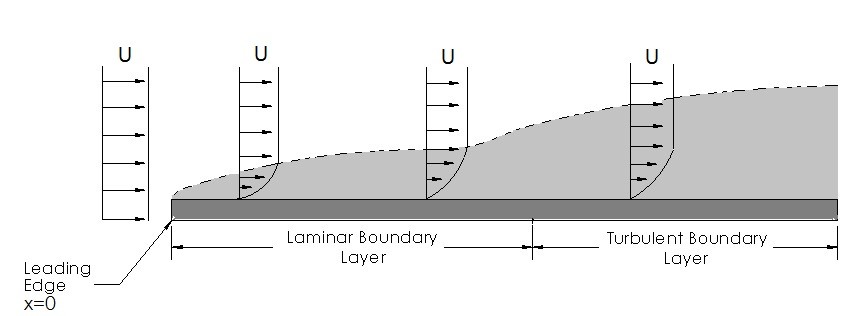
To determine if the fluid has a laminar or turbulent flow as it moves over the object Reynolds number would be used. Depending upon the surface roughness, the transition from laminar flow to turbulent flow occurs at a Reynolds number of 2X105 to 3X106. To calculate the Reynolds number for fluid flow over a flat plate the following equation would be used.
(Eq 1) $Re=\frac{Ux}{ν}$
U = fluid velocity
ν = kinematic viscosity
In addition to determining if the flow is laminar or turbulent Reynolds number also determines the importance of the viscous effects. As Reynolds number becomes larger the viscous effects aren’t as important at the front of the boundary layer, but become much more important as you near the end of the boundary layer. Also, the larger the Reynolds number the thinner the boundary layer becomes.
Boundary Layer Thickness
For the laminar part of the boundary layer it is possible to calculate the boundary layer thickness using the Blasius Equations. The reason why you may want to know the thickness of the boundary layer is because outside of the boundary layer the fluid particles will not be effected by viscous forces. To calculate the boundary layer’s thickness the following equation and table would be used.
(Eq 2) $δ=5\sqrt{\frac{νx}{U}},~\frac{u}{U}=0.99,~η=5.0$
δ = Boundary Layer Thickness
ν = Kinematic Viscosity
x = Length from the tip of the Edge
U = Fluid Velocity outside the boundary layer
u = Fluid Velocity inside the boundary layer at point of interest
Blasius Solutions for Laminar Flow
Wall Shear Stress
When the velocity profile of the boundary layer is determined it is possible to determine what the wall shear stress would be. Knowing what the wall shear stress is will make it possible to determine part of the drag forces that could be acting on the submerged object. To calculate the wall shear stress, using the Blasius equation, refer to equation 3.
(Eq 3) $τ_w=0.332U^{3/2}\sqrt{\frac{ρμ}{x}}$
τw = Wall Shear Stress
U = Fluid Velocity
x = Length of interest from Leading Edge
ρ = Fluid Densisty
μ = Dynamic Viscosity
Turbulent Boundary Layer
So far all that has been discussed is the laminar part of the boundary layer, since it can easily be represented through equations. The turbulent boundary layer however, is much more difficult to predict due to its randomness. The best way to think of the flow when it is turbulent is as a bunch of intertwined eddies of different sizes and different velocities. Due to what I just said, there is no exact answer for turbulent flow, however, computer models can be used to provide a prediction on what can be expected.