In a previous article I talked about inviscid flow. However, I did not include the assumption that the flow is irrotational. When this assumption is made the inviscid flow problems will be further simplified.
First, let’s take a look at the rotation of a fluid element. Mathematically, the rotation of a fluid element is equal to $\frac{1}{2}(∇×v)$. However, for an irrotational flow field $∇×v=0$. As a result, the curl of the velocity is equal to zero. By making this statement, it will allow us to state that for an irrotational flow field the vorticity will also be zero. Hence, the rotation of the fluid element around an axis, such as the z-axis, is expressed using the following equation.
(Eq 1) $ω_z=\frac{1}{2}\left(\frac{∂ν}{∂x}-\frac{∂u}{∂y}\right)=0$
Therefore,
(Eq 2) $\frac{∂ν}{∂x}=\frac{∂u}{∂y}$
(Eq 3) $\frac{∂w}{∂y}=\frac{∂ν}{∂z}$
(Eq 4) $\frac{∂u}{∂z}=\frac{∂w}{∂x}$
Uniform Irrotational Flow
Normal general flow would not be solvable using the above equations. However, uniform flow would. Uniform flow in the x-direction is illustrated in the image below.
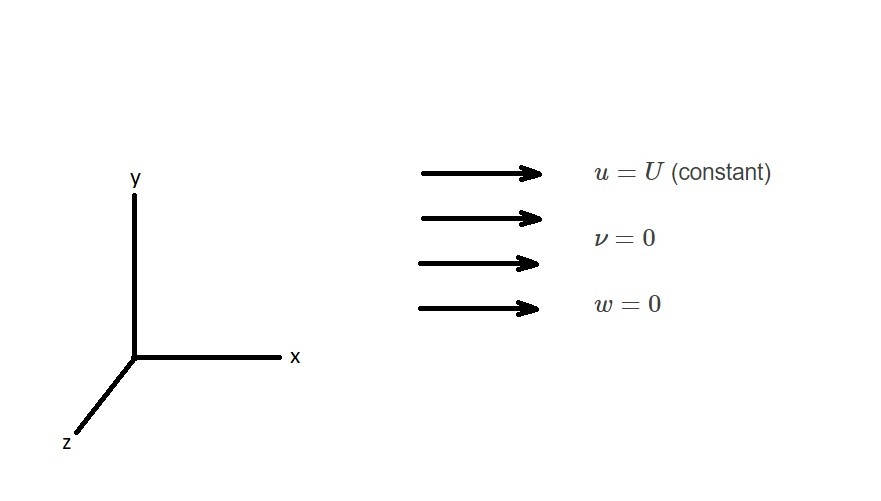
In this image it is stated that $u=U$ a constant, while $ν=0$ and $w=0$. Due to this fact, there will be no velocity gradients within the velocity flow field. In turn, this will result in irrotational flow.
Though uniform flow is very basic, it does occur in parts of different problems. For example as a fluid flows over an object, the flow will be uniform far way from the object. It can also be considered uniform at the entrance region of a pipe. Thus, for both cases the flow is also considered irrotational.
Irrotational Flow and an Inviscid Fluid
When a fluid is inviscid there will be no shear stresses on the fluid element. As a result, the only forces acting on the element will be due to pressure and weight. Now since the weight will act on the fluid center of gravity it will not be able to cause the element to rotate. In addition, pressure will act in a normal direction on the fluid element. Thus, neither pressure nor weight will cause the fluid element to rotate. Therefore, when the fluid is inviscid, it is safe to assume that is some parts of the flow field the fluid will have an irrotational flow.
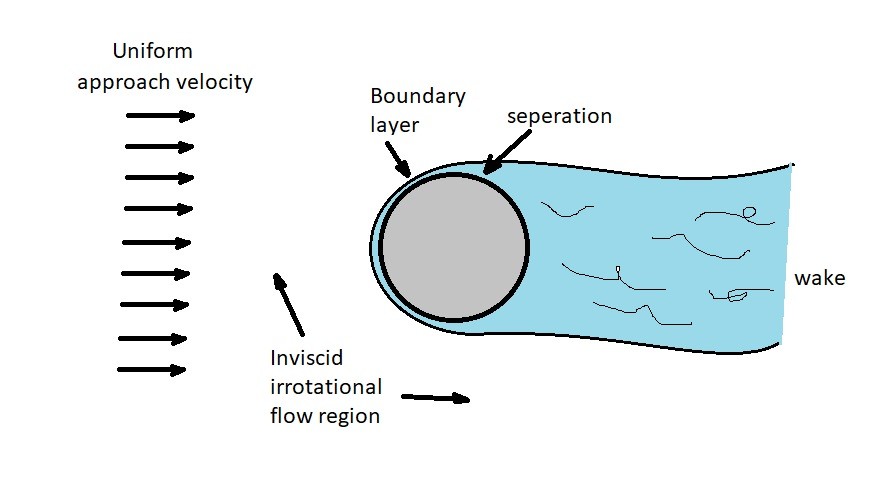
However, when there is a case of a rapid change in fluid velocity than this assumption can no longer be made. Again, an example of this would be fluid flowing over a submerged body. As the fluid approaches the body there is a rapid change in velocity causing a boundary layer to form. Inside the boundary layer the fluid can no long be considered irrotational. However, fluid outside the boundary layer can still be considered irrotational flow.
In addition to this, as the fluid flows past the submerged object, a wake will form downstream of that object. The wake represents the region inside the boundary layer that has slowed, or has random moving fluid.
Bernoulli Equation and Irrotational Flow
To use Bernoulli equation one of the assumptions that needs to be made is irrotational flow. When deriving the Bernoulli equation, the equation of motion are integrated along a streamline. The equation of motion that is integrated is as follows.
(Eq 5) $\frac{∇p}{ρ}·ds+\frac{1}{2}∇(v^2)·ds+g∇z·ds = [v×(∇·v)]·ds$
If we are able to assume that the flow is irrotational than the right side of this equation will go to zero. Taking this into consideration, and integrated the equation along a streamline, the following form of the Bernoulli equation will result.
(Eq 6) $\int{\frac{dp}{ρ}}+\frac{v^2}{2}+gz = c$
Furthermore, if we were to divide the above equation by the gravitational constant, and the fluid was incompressible with an irrotational flow, the Bernoulli equation will become the following.
(Eq 7) $\frac{p_1}{γ}+\frac{v_1^2}{2g}+z_1=\frac{p_2}{γ}+\frac{v_2^2}{2g}+z_2$
The above equation is meant to analyze a fluid between two points in the flow field. In order to use this equation the following assumptions must be satisfied. First, the flow must be inviscid. Second, the flow must be steady. Third, the fluid must be incompressible. Finally, fourth, the flow must be irrotational.