In past articles I have talked about the pressures a fluid can experience when it is completely at rest. However, there are cases where a fluid could be in motion but behave like a rigid body. In other words it would have rigid body motion. A fluid that is experiencing rigid body motion will not experience any shear stress. As a result the following general equation can be used to represent the pressure variations within the fluid.
(Eq 1) $-∇p-γ\hat{k} = ρa$
$γ$ = specific weight
$∇p$ = pressure gradient
$ρ$ = density
The above equation can be broken up into the following rectangular coordinates to express the pressure change over a certain distance in the x, y, and z directions.
(Eq 2) $-\frac{∂p}{∂x}=ρa_x$, $-\frac{∂p}{∂y}=ρa_y$, $-\frac{∂p}{∂z}=γ+ρa_z$
An example of a fluid that would be experiencing rigid body motion would be a glass of water in a car. When the car accelerates along a straight path, the water inside the glass will move as a rigid mass once the initial sloshing of the water settles down. Once the water inside that glass starts to move as a rigid mass there will be no shear stress within the fluid. As a result you will be able to use equations 1 and 2 to calculate the pressure variations of the water inside the glass.
Linear Motion
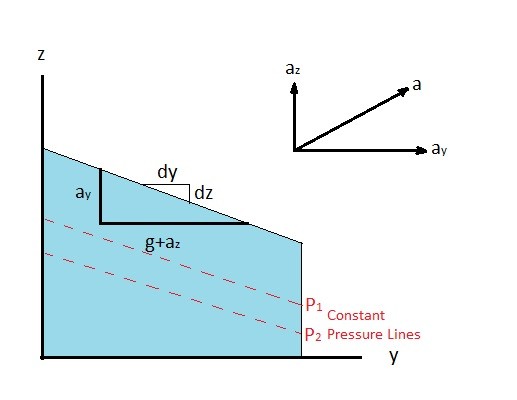
There are two types of motion that a fluid can experience without experiencing shear stress. These two types of motion are straight linear motion and rigid body motion around a fixed axis. First, lets return to the example above where there is a glass of water inside a car that is accelerating in a straight line. This is an example of linear motion. For linear motion to apply the direction of motion must be in a straight line. For simplicity I am going to say there is no motion in the x-direction, so that we only have to consider the pressure change in the y and z direction. In turn, equation 1 can be modified to the following.
(Eq 3) $dp = \frac{∂p}{∂y}dy + \frac{∂p}{∂z}dz$
or
$dp = -ρa_ydy-ρ(g+a_z)dz$
If you were analyzing the pressure along a line of constant pressure than $dp$ will equal 0. As a result equation 3 can be simplified to the following.
(Eq 4) $\frac{dz}{dy}= -\frac{a_y}{g+a_z}$
Lastly, there can be cases where linear motion will occur in the z-direction only. If this is the case than the pressure variation equation would be the following.
(Eq 5) $\frac{dp}{dz}=-ρ(g+a_z)$
Note that the resulting pressure from equation 5 is a combination of both hydrostatic pressure as well as acceleration on the z-axis.
Rigid Body Rotation
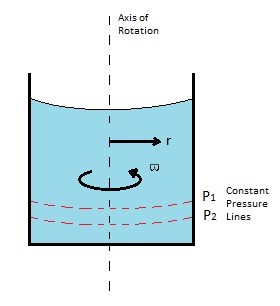
In addition to linear motion, a fluid can act like a rigid body when the container that contains it is spinning at a constant angular velocity $ω$ around a fixed axis. This will occur after the initial start up transient. In order to determine the pressure variation due to rotation about a fixed axis you will need to break up the general equation of motion, equation 1, into cylindrical polar coordinates. These equations will represent the pressure difference along the radius (r), the angle (θ), and the fluid depth (z).
(Eq 5) $∇p = \frac{∂p}{∂r}\hat{e_r} + \frac{1}{r}\frac{∂p}{∂θ}\hat{e_θ}+\frac{∂p}{∂z}\hat{e_z}$
where for rotation about a fixed axis
$a_r=-rϖ^2\hat{e_r}$, $a_θ = 0$, $a_z = 0$
$ϖ$ = angular velocity
thus
$\frac{∂p}{∂r}=ρrϖ^2$, $\frac{∂p}{∂θ}=0$, $\frac{∂p}{∂z}=-γ$
From the above equations it can be concluded that the pressure difference caused by rotation about a fixed axis is derived from the pressure difference along the radius and pressure difference due to fluid depth. As a result equation 5 can modified to the following equation.
(Eq 6) $dp = \frac{∂p}{∂r}dr + \frac{∂p}{∂z}dz$
or
$dp = ρrϖ^2dr-γdz$
after integration
$p = \frac{ρϖ^2r^2}{2}-γz + c$
$γ$ = specific weight
$c$ = constant (a specified pressure at some arbitrary point)
For rigid body rotation there are parabolic surfaces where constant pressure will occur. As a result $dp$ will equal 0. Taking this into account equation 6 can be modified to take inconsideration of a surface of constant pressure.
(Eq 7) $\frac{dz}{dr}=\frac{rϖ^2}{g}$
after integration
$z = \frac{ϖ^2r^2}{2g}+c$
$g$ = gravitational constant