In the previous article I discussed how to find the hydrostatic forces on a planar surface. However, not all surfaces are flat. Some are curved. An example of a curved surface would be the inside of tank and also the inside of pipes. As a result you will also need to know how to calculate the hydrostatic for on a curved surface. It is possible to derive the the resultant hydrostatic force on a curved surface through integration. This however can be tedious and is not normally simple. To work around this problem we will instead consider the equilibrium of the fluid volume interacting with the curved surface in terms of horizontal and vertical forces
For example lets take a look at the image below. In the image below fluid is interacting with a curved surface at the bottom of lets say a tank.
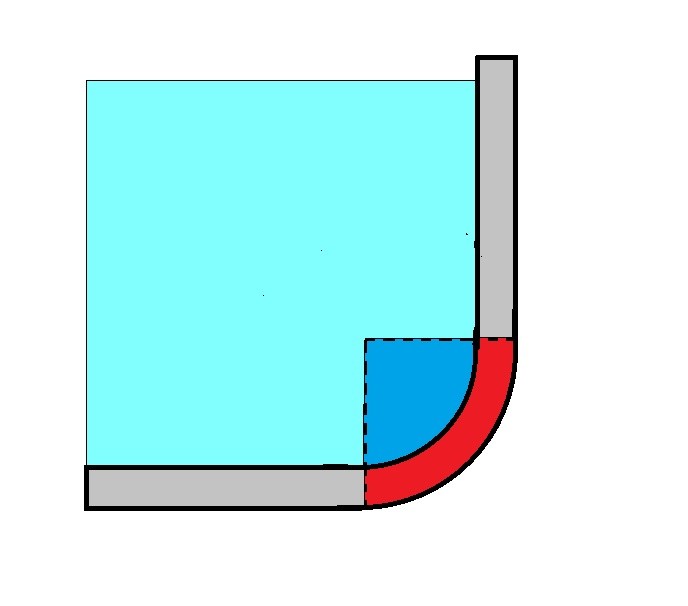
To find the hydrostatic force on the curved surface we will need to isolate the curved surface from the problem and draw a free body diagram.
.
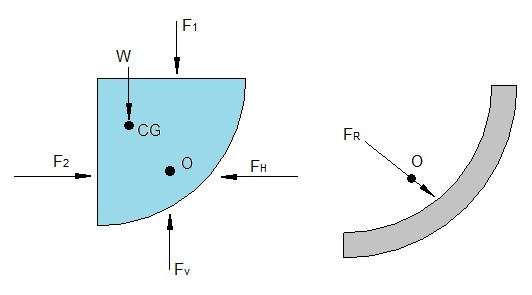
In the free body diagram forces $F_1$ and $F_2$ are determined from the relationships to the planar surface and the planar surfaces centroid. While $W = γV$ where $γ$ is the specific weight of the fluid and $V$ is the volume of fluid within the curved surface. Finally, the last step will be to sum the horizontal and vertical forces. Once you’ve done that you can find the magnitude of the horizontal and vertical forces.
(Eq 1) $F_H=F_2$
(Eq 2) $F_v=F_1+W$
(Eq 3) $F_R=\sqrt{F_H^2+F_v^2}$
The location O where the resultant force will make contact with the surface can be determined by summing the moments around an appropriate axis.