When discussing a pressure we are considering a normal force over a certain area, at a given point, within a specific plane of a fluid mass of interest. Now the question is will the pressure on a certain point vary with the orientation of the plane that passes through the point of interest? To answer this question we can determine the pressure on a point within a specific fluid element. In this case the fluid element will be a wedge shape.
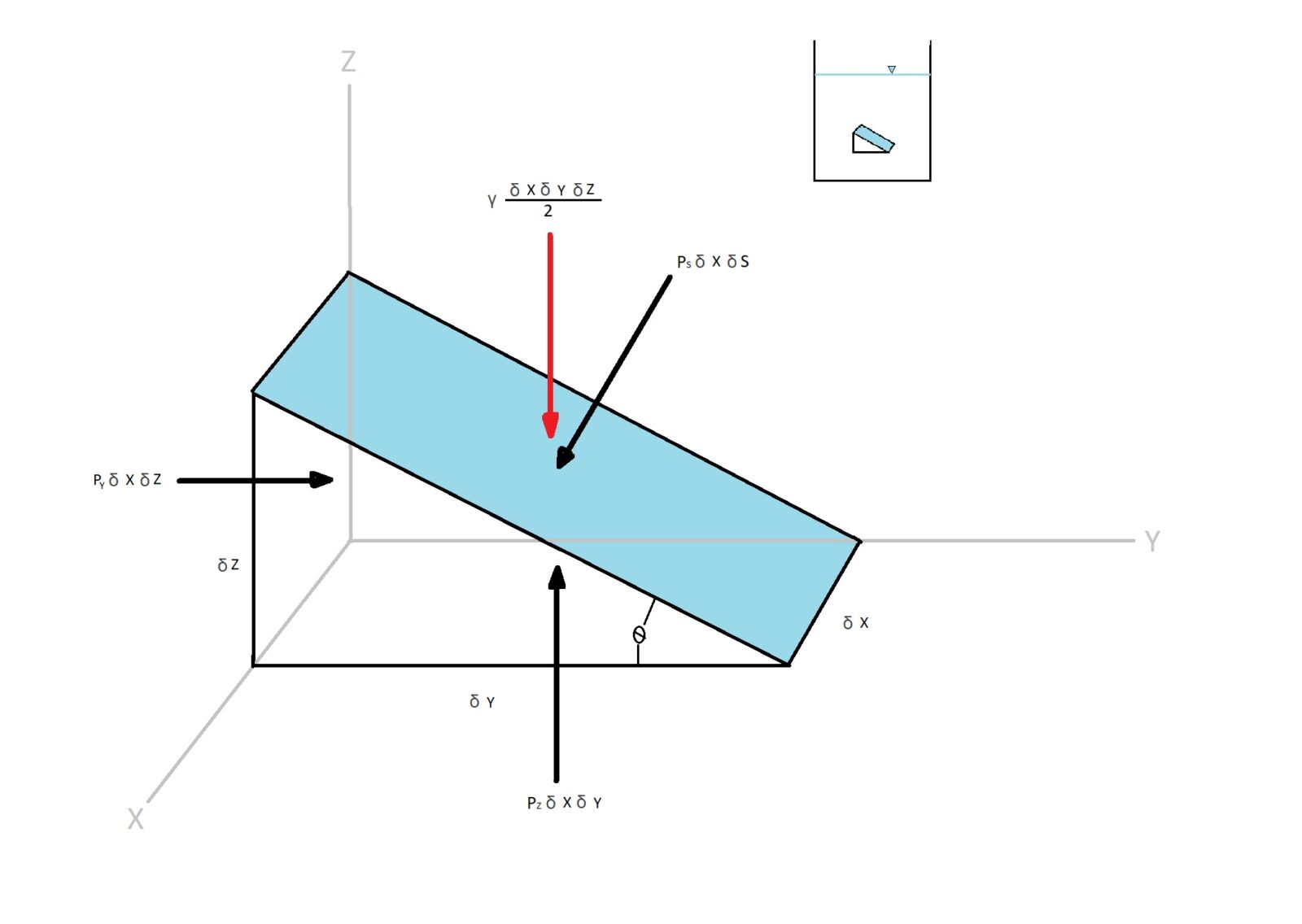
Shearing stresses will not be present for the above situation. As a result the external forces acting on the wedge are only due to pressure and specific weight of the fluid. For the above example I am only considering the forces in the z and the y directions for simplicity. To determine the force equations for the above example Newton’s second law of motion, F = ma will be applied.
(Eq 1) $ΣF_y = p_yδxδz – p_sδxδssinθ = ρ\frac{δxδyδz}{2}a_y$
$a_y$ = acceleration in the y-direction
$ρ$ = density
(Eq 2) $ΣF_z = p_zδxδy – p_sδxδscosθ-γ\frac{δxδyδz}{2} = ρ\frac{δxδyδz}{2}a_z$
$a_z$ = acceleration in the z -direction
$γ$ = specific weight
The above equations can be simplified when you take in consideration that $δ_y = δ_scosθ$ and $δ_z = δ_sinθ$. This will result in the following equations.
(Eq 3) $p_y – p_s = ρa_y\frac{δy}{2}$
(Eq 4) $p_z-p_s = (ρa_z+γ)\frac{δz}{2}$
Finally, if you were to allow $δx$, $δy$, and $δz$ to go to zero than $p_y = p_s$ and $p_z = p_s$. Hence it can be concluded that the pressure at a point will have $p_s=p_y=p_z$. This means that regardless of what θ is the pressure at a point for ” a fluid at rest, or in motion, is independent of direction as long as there is no shearing stress present” according to Pascal’s law. If shearing stress is present than the above statement will not hold true.