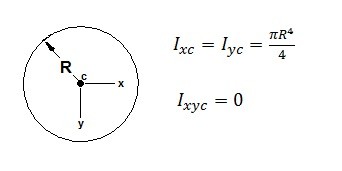If you were to submerge an on object into a fluid forces will develop onto the surface of the object. This is due to the pressure that is exerted on the object. For this article will be looking at hydrostatic force on a plane. Now why are we interested in hydrostatic force on a plane. Well the reason why is to prevent objects like dams, storage tanks, and ships from failing. It is also useful to determine the force required to open a gate that is controlling the water level of a reservoir.
When a fluid is at rest there will be no shearing stresses present within the fluid. As a result the forces caused by the pressure will perpendicular to the surface. In addition we know that the pressure caused by the fluid will change linearly in relation to the depth of the fluid. Due this fact the resulting pressure fields will result on the walls of a container.
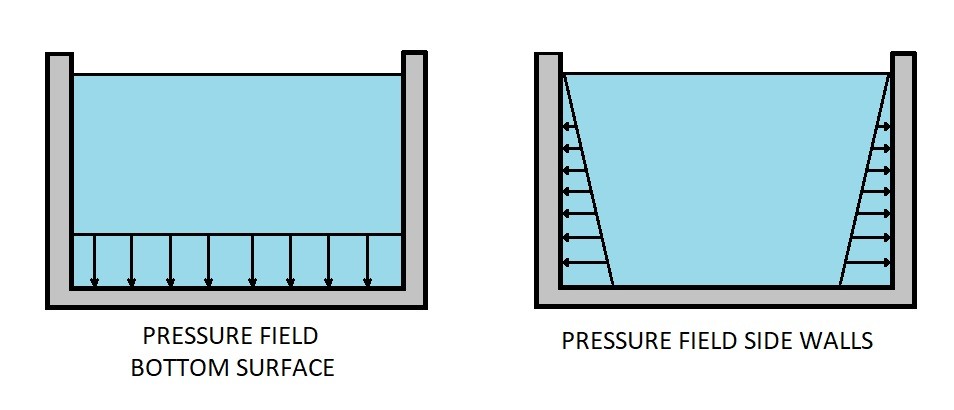
If the outside of the container is surrounded by atmospheric pressure then the pressure fields inside the container can be calculated using the following equation.
(Eq 1) $p=γh$
$γ$ = specific weight
$h$ = fluid height
Next a resultant force and where that resultant force is located will need to be determined to show how the pressure field will effect the surface of the container. For the image above the pressure is uniformly distributed over the bottom of the container. As a result the resultant force will pass through the centroid of the area. On the other hand the pressure on the sides of the container is not uniformly distributed. Do to this fact a process will need to be followed to determine what the resultant force is and where it is located on the sides of the container.
Resultant Force
The first step that will need to be taken is to determine what the resultant force. Since the pressure will be distributed over an area you will need to determine what area is as well as the geometry. You will also need to know if the surface you are analyzing is a vertical surface or if it is set at an angle. Once those are determined you will use the following equations to determine the resultant force.
(Eq 2) $F_R = \int_AγhdA = \int_AγysinθdA$
where $h = ysinθ$
The above equation is a general equation on how to find the resultant force acting the side wall of a container. On the other hand if you know where the centroid of the surface area and what the area is than you can simplify the above equation to the following.
(Eq 3) $F_R = γAy_csinθ$ if the wall isn’t vertical
or
$F_R = γh_cA $ for vertical walls
$h_c$ = vertical distance to the centroid from the fluid surface
Be aware that the magnitude of the force does not depend on the angle of the wall. Instead it depends on the specific weight of the fluid, the total surface area of the wall, and how far the centroid is from the fluid surface.
Resultant Force Location
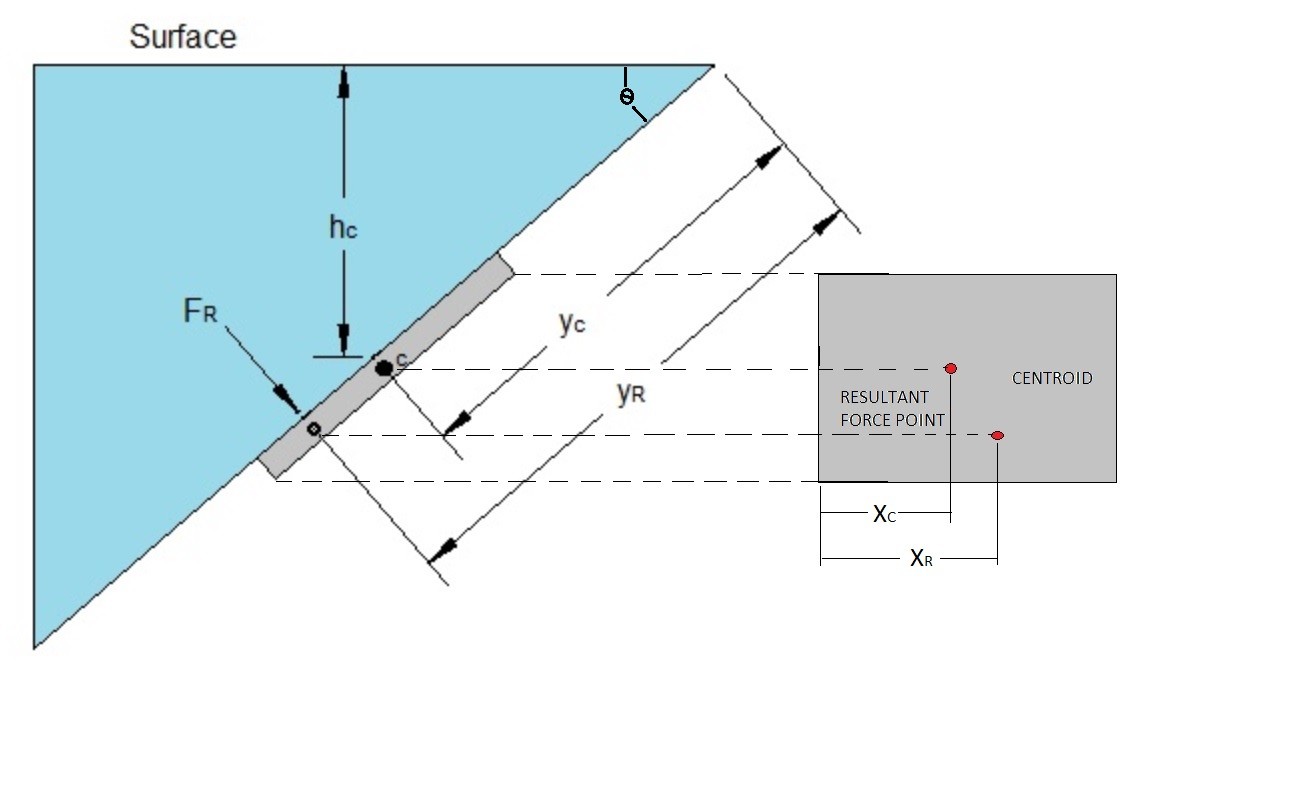
The next thing that needs to be determine is at what point will the resultant force pass through the wall. Intuition may tell you that it would be at the centroid of the area, however that is not the case. Instead you will need to find the x coordinate ($x_R$) and y coordinate ($y_R$) by summing the moments around the y axis and the x axis. This is done by finding the area moment of inertia around the centroid. The resulting equation for the x coordinate and y coordinate can be seen below.
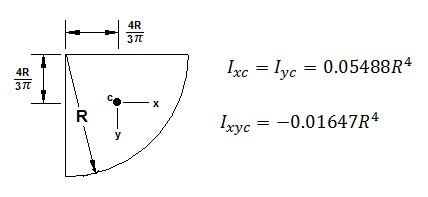
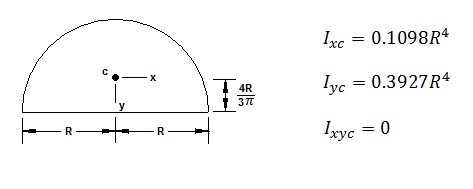
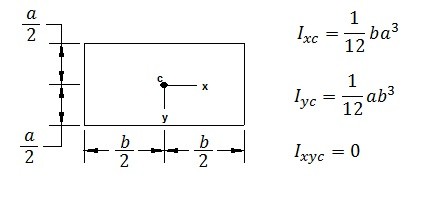
(Eq 4) $x_R = \frac{I_{xyc}}{y_cA}+x_c$
(Eq 5) $y_R = \frac{I_{xc}}{y_cA}+y_c$
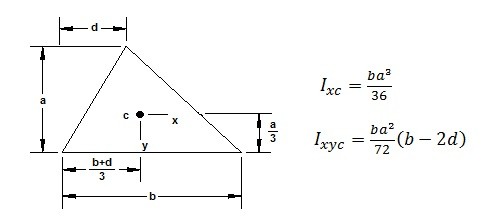
Area Moment of Inertia and Centroids of Common Shapes