Recall from the previous article that the general equation of motion for a fluid is $-∇p-γ\hat{k}=ρa. However, for a fluid at rest the acceleration of the fluid will be zero. This will allow you to modify the general equation of motion to the following equation.
(Eq 1) $∇p+γ\hat{k}=0$
Further if you were to break the above equation into is component form than you would have the following.
(Eq 2) $\frac{∂p}{∂x}=0,~\frac{∂p}{∂y}=0,~\frac{∂p}{∂z}=-γ$
$γ$ = specific weight
Equation 2 shows that pressure does not depend on x and y. Instead pressure is only determined by the weight of the fluid in the z-direction, where the z-direction represents fluid depth. As a result the general differential equation that is used to find the pressure of a fluid at rest is as follows.
(Eq 3) $\frac{∂p}{∂z}=-γ$
Incompressible Fluid
Recall that an incompressible fluid is a fluid that requires a considerable amount of pressure to noticeably change its volume and density. To determine whether a fluid can be considered incompressible you will need to see what its bulk modulus is. Liquids are generally always considered incompressible under normal circumstances. If you have an incompressible fluid than you can directly integrate equation 3 as seen in the following equation.
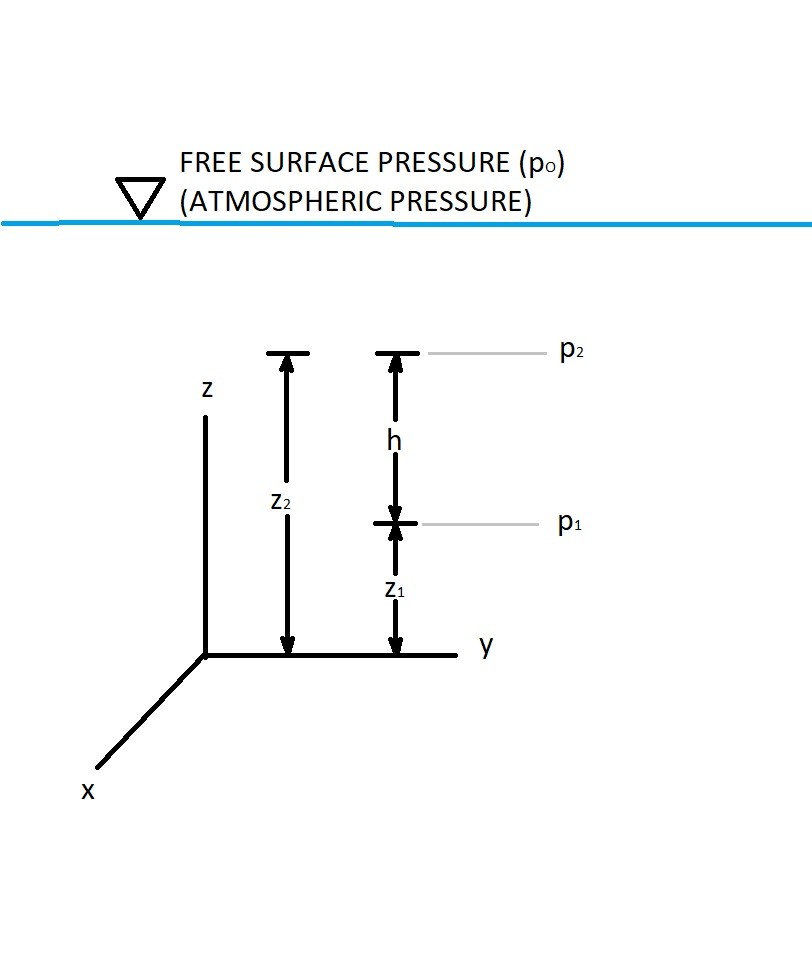
(Eq 4) $\int^{p_2}_{p_1}dp=-γ\int^{z_2}_{z_1}dz$
where
$p_2-p_1 = -γ(z_2-z_1)$
or
$p_1 = γh + p_2$
$h$ = fluid height or pressure head
You should notice from equation 4 that the resulting pressure ($p_1$) is only a product of fluid height. Due this fact pressure will only increase due to fluid depth and fluid volume does not effect the resulting pressure. This is commonly called hydrostatic distribution.
Finally, though rare, when you are calculating the specific weight of a fluid, you might have to see if the gravitational constant g has significantly changed. The reason why is because specific weight is a product of both fluid density and gravitational acceleration. However, the only time you might have to consider a change in gravitational acceleration would be if you were calculating the pressure at a deep section of ocean floor. If this were the case though, you would most likely also have to consider a change in density from the ocean surface to the ocean floor due to the large increase in pressure.
Compressible Fluid
Compressible fluids are fluids that’s density can change significantly with a change in pressure and temperature. Gas is generally always considered a compressible fluid. One way to solve a problem that has a compressible gas is to use the ideal gas law.
(Eq 5) $ρ = \frac{p}{RT}$
$R$ = Ideal gas constant
$T$ = Absolute Temperature
Using the ideal gas law you will be able to modify equation 3 to find the pressure variation in gas when it is at rest.
(Eq 6) $\frac{dp}{dz} = -\frac{gp}{RT}$
where
$\int_{p_1}^{p_2}\frac{dp}{p}=-\frac{g}{R}\int_{z_1}^{z_2}\frac{dz}{T}$
After completing the integration in equation 6 the resulting equation will follow. To use this equation isothermal conditions will need to exist.
(Eq 7) $p_2 = p_1exp\left[- \frac{g(z_2-z_1)}{RT_o} \right]$
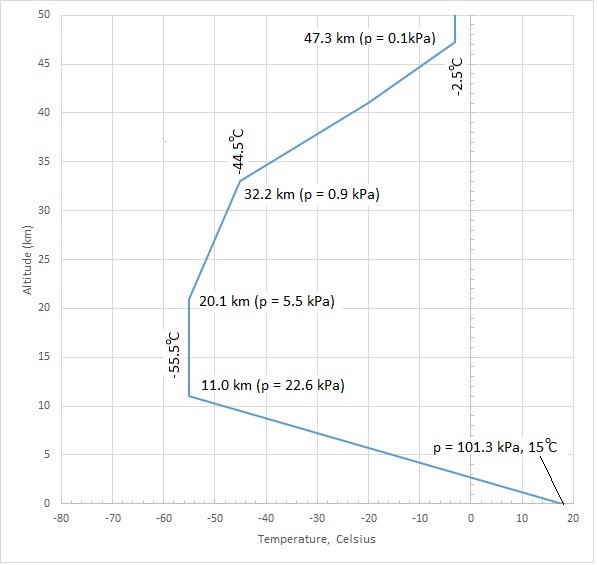
Atmospheric Pressure
A standard atmospheric pressure is used to determine the effect the earth’s atmosphere will have on a hydrostatic problem. However, since a gas’s pressure will vary with pressure as well as temperature, so will the atmospheric pressure. Below is a graph showing how the standard atmospheric pressure changes as altitude and temperature changes.