A submerged or partially submerged object in a fluid will have resultant force acting on it called the buoyant force. The buoyant force will determine the buoyancy of an object. Specifically the buoyant force is net vertical force on an object. It will increase as the submersion depth increases due to the pressure increasing. To determine this force you can use similar steps that you would use to find hydrostatic force on a curved surface. As a result the buoyant force for some arbitrary object would be expressed in the following free body diagram.
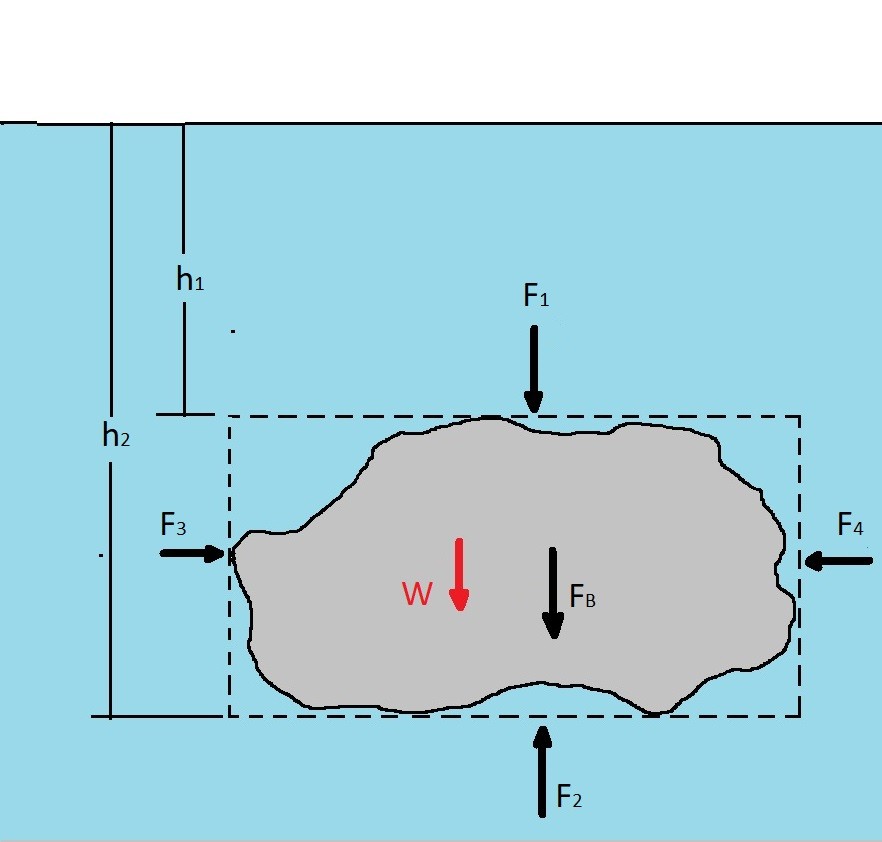
(Eq 1) $F_B = F_2 – F_1 – W$
$W$ = weight of the fluid in the dotted box minus the body
$F_B$ = Force the body exerts on the fluid
or
$F_B = γ(h_2-h_1)A-γ[(h_2-h_1)A-V]$
$V$ = Volume of the body
$γ$ = specific weight of fluid
$A$ = horizontal area of the upper and lower surface
The above equation can be simplified to the following equation.
(Eq 2) $F_B = γV$
Equation 2 represents that buoyant force on the body which is the force the fluid will impose on the body. As a result the direction of the buoyant force will be in the opposite direction of what is seen in the free body diagram. As a result by Archimedes’ principle ” the buoyant force has a magnitude equal to the weight of the fluid displaced by the body and is directed vertically upward.”
Center of Buoyancy
Next you may need to find the center of buoyancy. Specifically the center of buoyancy represents the point in the body where the buoyant force acts. As a result it can be found by summing the moment of the forces.
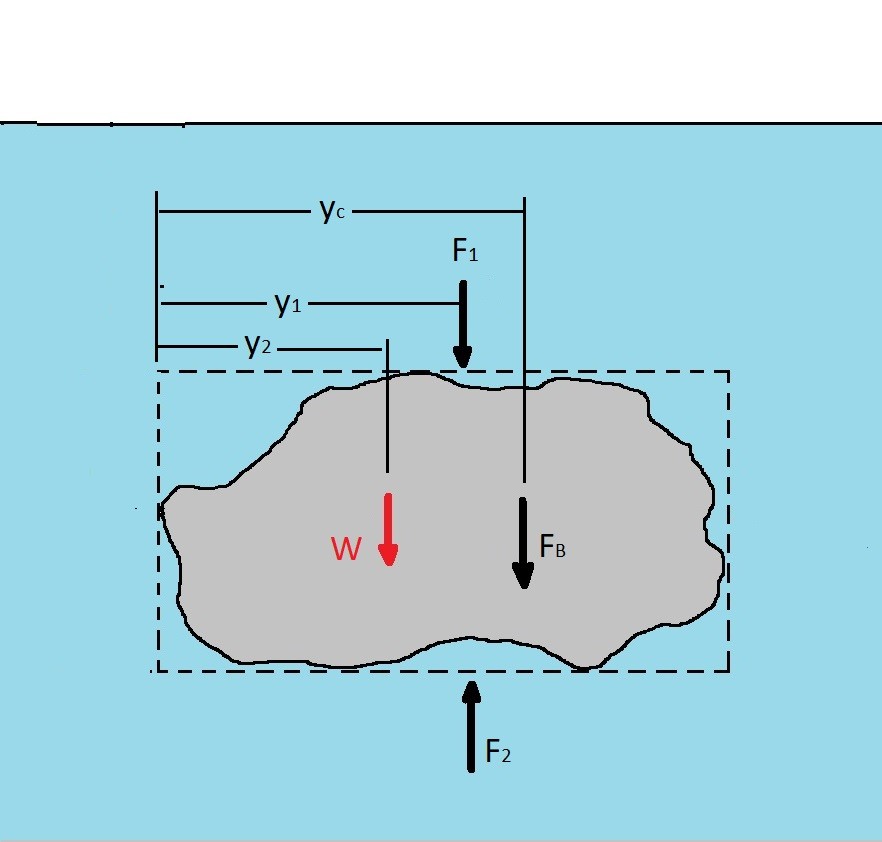
(Eq 3) $y_c=\frac{F_2y_1-F_1y_1-Wy_2}{F_B}$
Stability
Another concern that you should have is how stable a floating object is while it is floating. In other words you don’t want to have, say ship, capsize because it wasn’t stable. However to determine if an object is stable or not is quite simple. It all depends on where center of gravity (CG) is in comparison to where the center of buoyancy is. As a result if the center of gravity is lower than the center of buoyancy there will be restoring couple between the to forces. Thus the body can be considered to be in stable equilibrium. On the other hand if the center of gravity is higher than the center of buoyancy there will an overturning couple between the two forces. Hence there will be an unstable equilibrium.
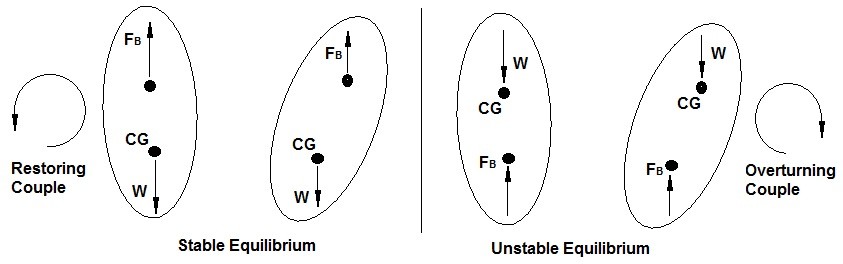
To help prevent unstable equilibrium on large ships that would otherwise be top heavy, the ship will purposely take in water in its ballast tanks to lower its center of gravity.