As seen in the last section we can conclude that the pressure at a single point is independent of direction when there are no shearing stresses present. However, next we need to determine how the pressure of a fluid will vary from one point to the other when there is no shearing stresses present. In essence creating a pressure field.
Let’s start by looking at a basic cubic fluid element. On this element there are two different type of forces that are interacting with it. They are surface forces and body forces. Surface forces are caused by the external pressures acting on the element. While body forces consider the weight of the element caused by the specific weight of the fluid.
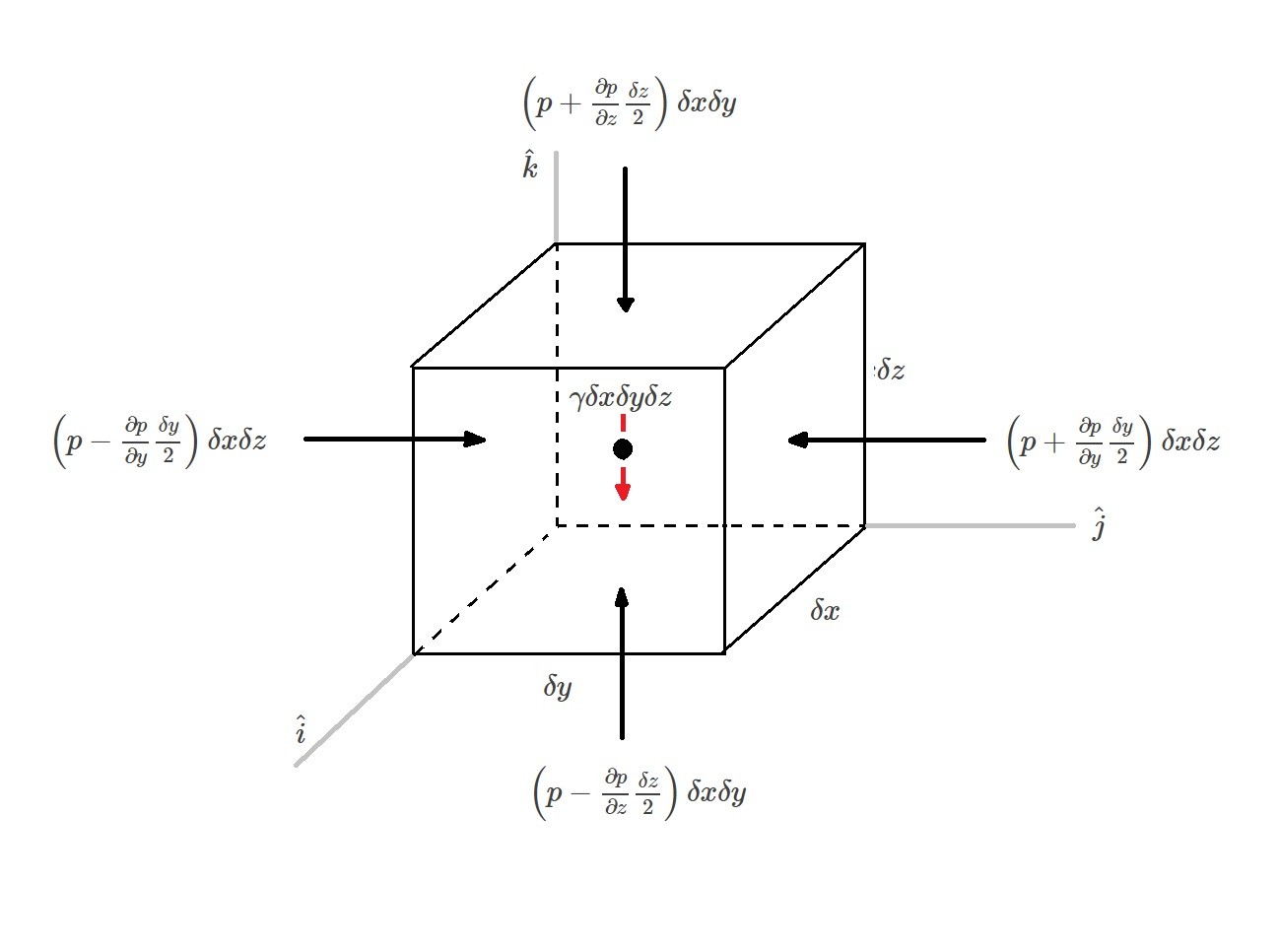
Surface Forces
First let take a look at the surface forces on the fluid element shown above. The different surface forces are caused by a pressure (p) on the face of the element. The average pressure on each face is a product of the pressure and its derivative. As δx, δy, and δz approach zero, higher order terms can be removed from the equation. The equation below represents the resultant force in the y-direction.
(Eq 1) $δF_y = \left(p-\frac{∂p}{∂y}\frac{δy}{2}\right)δxδz-\left(p+\frac{∂p}{∂y}\frac{δy}{2}\right)δxδz$
or
$δF_y=-\frac{∂p}{∂y}δxδyδz$
From the above the resultant forces in the x and z can be determined to be the following.
(Eq 2) $δF_x=-\frac{∂p}{∂x}δxδyδz$
(Eq 3) $δF_z=-\frac{∂p}{∂z}δxδyδz$
Finally, the above equations can be combined and expressed in vector form.
(Eq 4) $F_R = δF_x\hat{i}+δF_y\hat{j}+δF_z\hat{k}$
or
$\frac{∂p}{∂x}\hat{i}+\frac{∂p}{∂y}\hat{j}+\frac{∂p}{∂z}\hat{k}=∇p$
where
$\frac{δF_R}{δxδyδz}=-∇p$
Body Forces
Next, we are going to have to consider any body forces effecting the fluid element. In this case the force would be the weight of the fluid element caused by the specific weight of the fluid.
(Eq 5) $-δW\hat{k} = γδxδyδz\hat{k}$
$γ$ = specific weight
Finally, using Newton’s second law of motion $F=ma$ the surface forces and body forces of the fluid element can be combined.
(Eq 6) $-∇p – γ\hat{k} = ρa$
$ρ$ = Fluid Density
$a$ = acceleration
Equation 6 represents the general equation of motion for a fluid element when there is no shear stresses present on the fluid element.