As stated previously a rigid body can see two basic states of motion, translation and rotation about fixed axis. To calculate the force of a body that is translating you would simply use F=ma. On the other hand a body that is rotating and has a rotational velocity that is changing due to an angular acceleration will develop a moment instead of a Force. The moment is a product of the mass moment of inertia and the angular acceleration. In turn mass moment of inertia is the resistance to the angular acceleration.
Mass moment of inertia is a mechanical property of motion that is normally represented by symbol $I$. It takes both the mass of the body as well has the distance the mass is from axis of rotation of the rigid body into consideration. The further the mass is from the center of rotation or the greater the mass is will increase the total mass moment of inertia.
Moment of Inertia of a Rigid Body
All rigid bodies have a mass moment of inertia that is based off of its center of mass. To determine mass moment of inertia you would take the integral of the second moment of the rigid body where $dm$ represents the mass of all of the element that make up the body. You can use the general equation below to find a body’s mass moment of inertia around a single axis such as the z-axis. However, whic ever axis you choose must go through the bodies center of mass.
(Eq 1) $I=∫_mr^2dm$
where r represents the “moment arm” which is the perpendicular distance from the axis going through center of mass in respect to $dm$.
In some cases you might have a variable density of the material. When this is the case you can modify equation 1 to the following equation so that you are integrating using volume elements.
(Eq 2) $I=∫_Vr^2ρdV$
On the other hand there can cases where the density is constant. If this is the case you will not have density as part of the integration. This will cause integration to be purely a function of geometry.
(Eq 3) $I=ρ∫_Vr^2dV$
You will have to perform a triple integration when you are using volume elements.
where
dV = dxdydz
Moment of Inertia of a Rigid Body rotating about a Fixed Axis
Unless a rigid body is rotating around its center of mass, the mass moment of inertia of a system will not be the same as the mass moment of inertia of the rigid body itself. Instead it will be a combination of the mass moment of inertia of the rigid body and the distance the center of mass is from the axis of rotation. The greater the distance from the axis of rotation the larger the mass moment of inertia will become. This is why figure skaters spins they slow down when they spread their arms and speed up when they bring their arms in towards their bodies. Use the equation below to calculate the mass moment of inertia of a rigid body rotating around a fixed axis.
(Eq 4) $I = I_a+md^2$
where
$I_a$ = Objects moment of inertia
$d$ = distance from the fixed axis of rotation
$m$ = mass of the rigid body
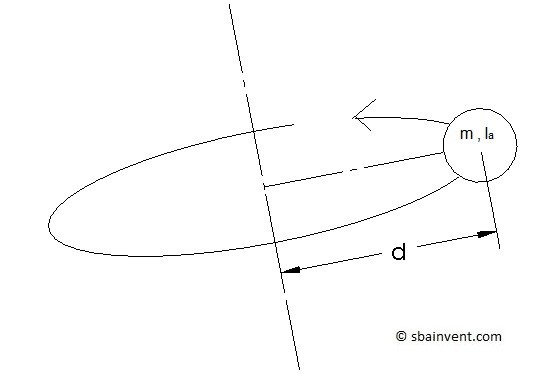
The parallel axis theorem was used to derive the equation above. Below is the general equation of the parallel axis theorem.
(Eq 5) $I=∫_mr^2dm$$=∫_m[(d+x’)^2+y’^2]dm$$=∫_m(x’^2+y’^2)dm+2d∫_mx’dm+d^2∫_mdm$
Radius of Gyration
Sometimes a textbook will state the radius of gyration instead of the mass moment of inertia. However, if you know the mass of the object you can converted radius of gyration to mass moment of inertia by using the following equation.
(Eq 6) $I = mk^2$
where
$k$ = radius of gyration
Mass Moment of Inertia of Basic Shapes
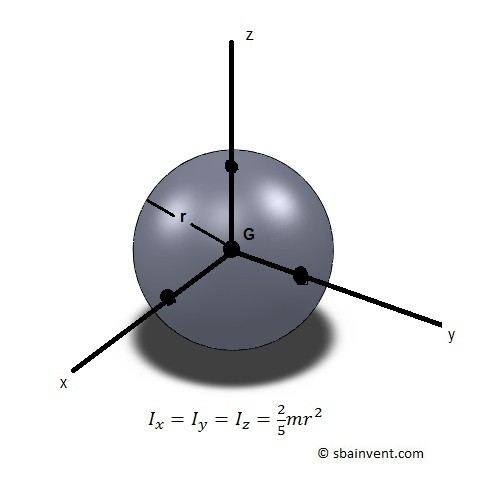
Sphere
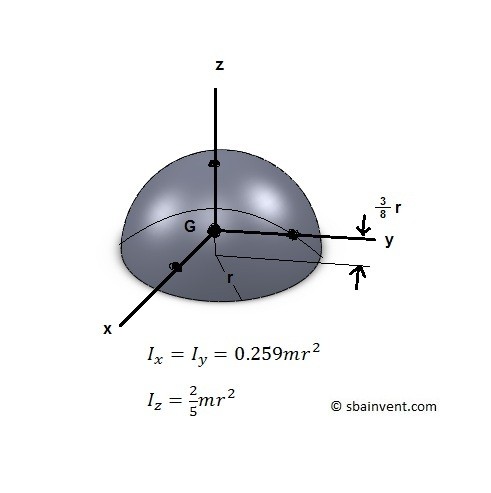
Hemisphere
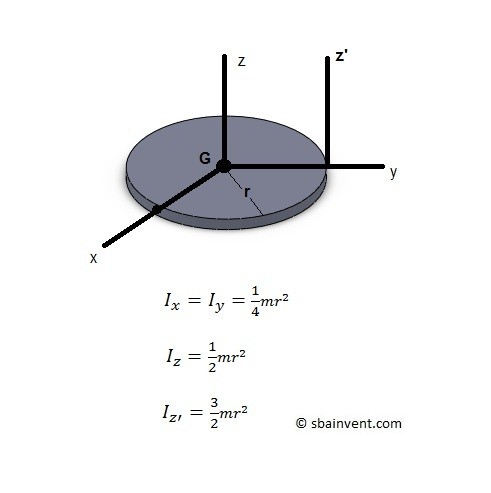
Thin Disk
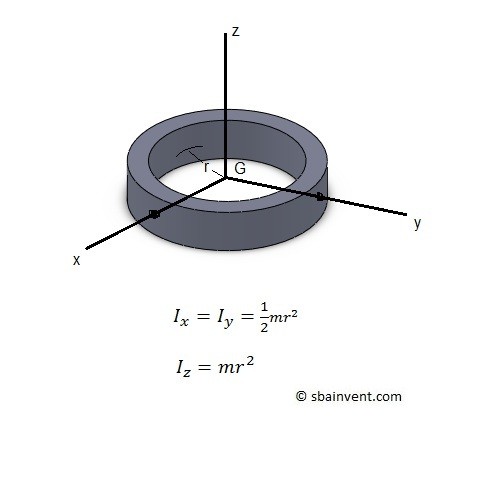
Thin Ring
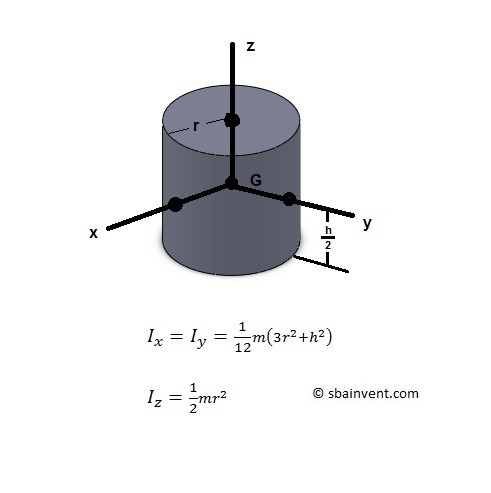
Cylinder
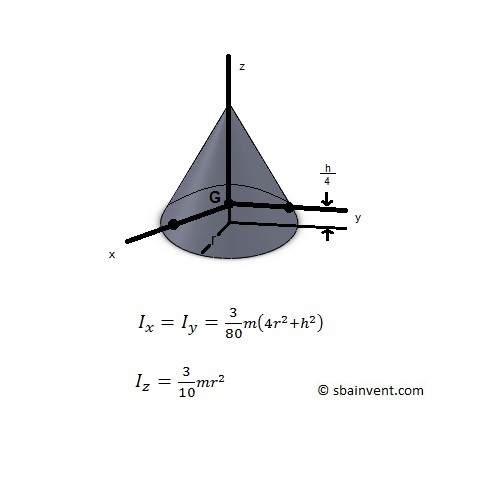
Cone
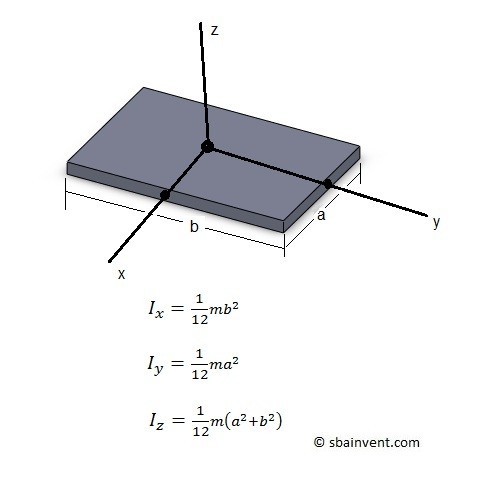
Thin Plate
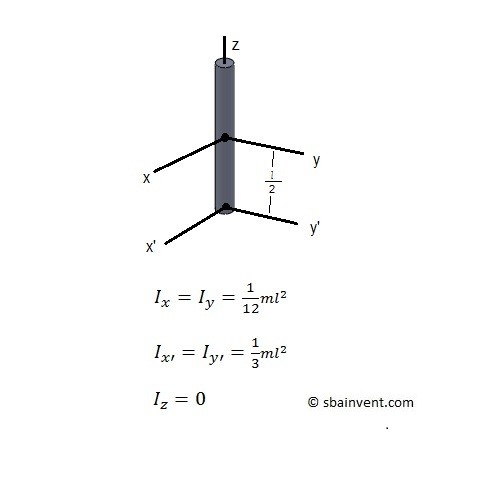
Slender Rod